機械学習を勉強していく中でたまに「次元の呪い」という言葉を見かけますよね。調べていても「ベクトルの次元が大きすぎると〜」のように数学的な表現がすぐに出てきて抵抗がある方も多いことでしょう。本記事ではそういった方を対象に「次元の呪い」はどういった現象で何が問題となってくるのかを解説していきます。
「次元の呪い」とは
まずは次元の呪いに関するWikipediaの日本語記事を見てみましょう。
次元の呪い(じげんののろい、英: The curse of dimensionality)という言葉は、リチャード・ベルマンが使ったもので、(数学的)空間の次元が増えるのに対応して問題の算法が指数関数的に大きくなることを表している。
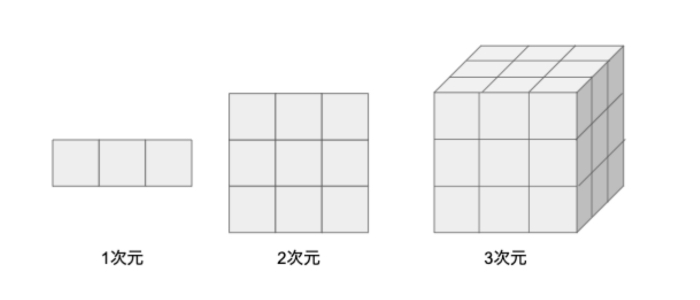

この図では1次元、2次元、3次元にそれぞれ3要素ずつ配置したものです。各次元の要素の総数を数えてみましょう。
- 1次元:3要素 × 1次元 = 3要素
- 2次元:3要素 × 2次元 = 9要素
- 3次元:3要素 × 3次元 = 27要素
次元の増加に伴って要素の数が3倍ずつ大きくなっていっていることがわかります。この増加の仕方を指数的に大きくなるといいます。機械学習などの分野では扱うデータの次元が数千を超えることも少なくないので、このような状況では必要な計算の数が非常に大きくなってしまいます。これによって引き起こされる問題を「次元の呪い」といいます。
また高次元になればなるほどある点から近い点と遠い点との距離の差がなくなってくるといった問題もあります。
機械学習における次元の呪い
機械学習であるデータをクラス分類したり、クラスタリングしたい場合を考えてみましょう。
先ほどの章では高次元データになればなるほど、点と点の距離に差がなくなっていくといいました。距離がなくなるということは、分類が難しくなったり、クラスタに分けることが難しくなることを意味します。
それだけでなく次元が増加すると機械学習モデルが学習すべきパラメータの数も増加していくため、特にニューラルネットワークのようなモデルでは学習が遅くなることや予測が遅くなるといった問題が生じます。
まとめ
最後に「次元の呪い」についてもう一度まとめてみます。
- 次元の呪いは扱うデータの次元が大きくなればなるほど指数的に扱うデータの総量が増加するという問題
- データが高次元になれば、遠い点と近い点の距離に違いがなくなる
- 機械学習で利用するデータの次元が増えると「予測の難しさ」、「扱うパラメータ数の増加」といった問題が生じる




