AI（機械学習）について学びを深めていると、RMSEやRMSLEといった小難しい単語を目にしますよね。「これらは機械学習モデルの性能を評価する指標だよ」という一言で簡単に済ませることもできるのですが、具体的にそれぞれどんな特徴があってどんな場面で使ったら良いのか？まで細かく説明するとなると中々大変かもしれません。
実際僕自身ザックリとした使い方は理解しているつもりだったのですが、なぜこの場合はRMSEなのか？なぜこの場合はRMSLEなの？という疑問に答えられず、「いつも適当に対処してきたな」という自分にハッとしました。
そこで今回はRMSEをはじめとした回帰タスクにおける評価指標について基本から見直し、理解を深めることにしました。
そもそもRMSE（Root Mean Square Error）とは
そもそもRMSEとは、Root Mean Square Error（二乗平均平方根誤差）の略で、回帰モデルの最も一般的な性能指標で以下の式で表現されます。
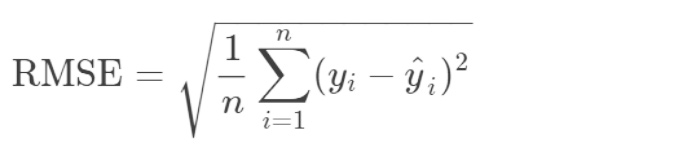
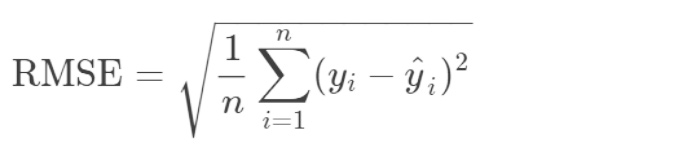
このRMSEが意味するものをザックリ言うと、実際の値と予測値のズレが小さければ小さいほど、当てはまりの良いモデルだって言えるよね、そのための指標がRMSEだよねと言うことです。もっと詳しく言えば、RMSEは「実際の値と予測値のズレの二乗の総和の平均値のルートをとったもの」となり、このRMSEが小さければ小さいほど機械学習モデルの性能が良いと判断できます。
RMSE（Root Mean Square Error）の特徴と使いどころ
回帰タスクで頻繁に使われるこのRMSE（Root Mean Square Error）ですが、次のような特徴があります。
＜RMSEの特徴と使いどころ＞
- 大きいエラー、間違いをより重要視する（実際よりも大きく予測した場合に大きなペナルティを与える）ため、大きな価格の誤差を許容できないケースに使用される
- 回帰モデルの最も一般的な性能評価指標であり、多くの場合はRMSEが使われる
- 観測値と計算値（予測値）の差を二乗している分、MAE（平均絶対誤差）に比べて外れ値にひきずられて著しく値が大きくなりやすい。そのため、事前に外れ値を除くなどしておかないと外れ値に過剰適合したモデルができる可能性がある
- 誤差がどれだけあるかを比率、割合ではなく幅で着目しているので、小さなレンジでの誤差に着目したい場合には適していない
＜参考＞MAE：Mean Absolute Error（平均絶対誤差）
MAE（Mean Absolute Error：平均絶対誤差）もRMSE同様に回帰タスクで使われる評価指標の一つで、予測値と実際の値の絶対差の平均で表され以下の式で表現されます。
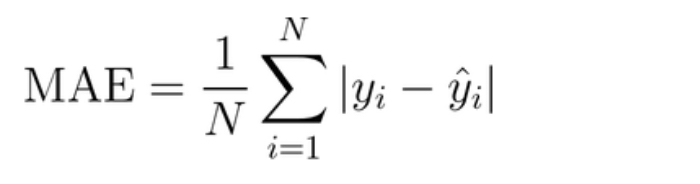
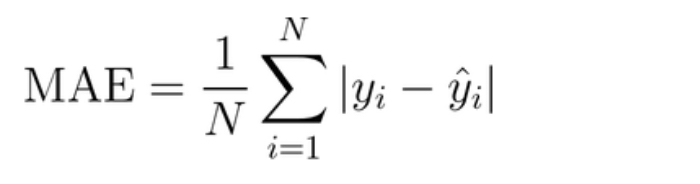
数式からわかるようにMAEは誤差を二乗していないので、RMSEに比べて外れ値の影響を受けにくい特徴があります。外れ値を多く含んだデータを扱う際には、RMSEよりもMAEを使うことが適していそうですね。
＜参考＞ RMSEとMSE(平均二乗誤差)
また、RMSEのルートを外したものはMSE（Mean Square Error、平均二乗誤差）と呼ばれています。
こちらもRMSE同様に、実際の値と予測値のズレ（誤差）がどれだけあるかを示しており、当然値がモデルの性能がどれだけ悪いかを示す指標の一つです。MSEもよく見かけますが、評価指標として一般的に使われるのはRMSEです。
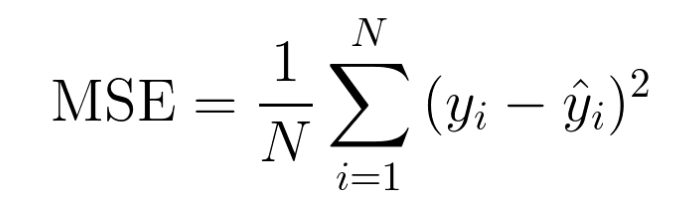
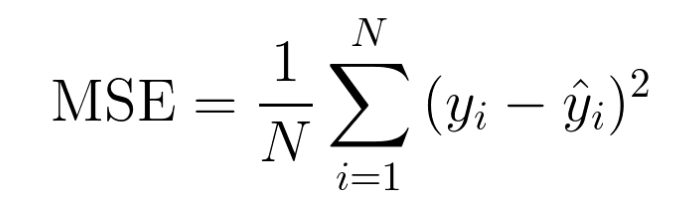
RMSEやMSEで最小値が求められる原理について、直感的に数式無しで理解したいという方に向けて以前記事を書きましたので必要な方は以下の記事もご参考ください。
RMSLE（Root Mean Squared Logarithmic Error）とは？
続いてRMSLE（Root Mean Squared Logarithmic Error）も回帰タスクにおける代表的な性能評価指標の一つです。RMSLEは予測値と実測値の対数差の二乗の総和の平均値のルートをとったもので以下の数式で表現されます。
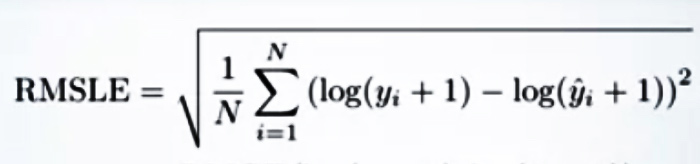
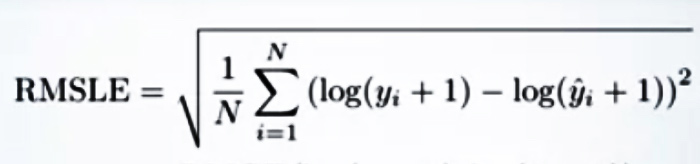
RMSLEは「対数平方平均二乗誤差」と呼ばれることもありますが、名称が長いのでRMSLEが一般的なようですね。対数をとる前に予測値と実測値の両方に＋１をしているのは、予測値または、実測値が0の場合に log(0) となって計算できなくなることを避ける目的があります。
RMSLEの特徴と使用時に注意したいこと
さて、ここで改めてRMSEとRMSLEのどちらを使ったら良いかという大きな疑問が出てきますが、調べてみると扱うデータによってRMSEよりもRMSLEを評価指標として使ったほうが良い場合があり、RMSLEには以下の特徴があるようです。
- 実際より少なく予測した場合に大きなペナルティ（損失）を与える（下振れを抑えたいケースに使用される）性質を持つため、来客数の予測や店舗の在庫を予測するようなモデルにおいてはRMSLEが用いられる。来客数を少なめに予測して仕入れや人員が不足して困ったり、出荷数を少なく見積もって在庫が余って困る等の状況を引き起こしたくない場合にRMSLEを使用
- ある値は10、ある値は10,000といった値の範囲が大きな場合（対数正規分布に近い分布、裾の重い分布を持ってスケール変換しないままだと大きな値の影響が強い場合）のデータの学習に利用
- Kaggleなどの分析コンペでは、目的変数の対数をとって変換した値を新たな目的変数とした上でRMSEを最小化するという形で、RMSLEを最小化する取り扱い方法が多い
- 実測値と予測値の誤差を幅ではなく比率や割合として表現したい場合、小さなレンジの誤差に着目したい場合に用いられる。RMSLEを表す数式の二乗括弧内の式において、log(実測値 + 1) – log(予測値 + 1 ) = log((実測値 + 1) / (予測値 + 1)) となることから、RMSLEは予測値と実測値の誤差の比率、割合に着目している
＜参考＞ RMSEとRMSLEを実際に比較してみる
ここまでは文章だけでRMSEとRMSLEの特徴について見てきましたが、ここからは実際にRMSEとRMSLEそれぞれに対して、共通の予測値と実測値を数値を入れて違いを確認していきましょう。
適当に値を準備して、Pythonを使ってRMSEとRMSLEを計算してみます。
まずはじめにRMSEとRMSLEの関数を準備します。
import numpy as np
from sklearn.metrics import mean_squared_error
# ---RMSEとRMSLE関数を準備
def rmse(y_true: np.ndarray, y_pred: np.ndarray) -> np.float64:
return np.sqrt(mean_squared_error(y_true, y_pred))
def rmsle(y_true: np.ndarray, y_pred: np.ndarray) -> np.float64:
rmsle = mean_squared_error(np.log1p(y_true), np.log1p(y_pred))
return np.sqrt(rmsle)
RMSLEは予測値が実測値よりも小さく振れた場合に大きくペナルティを課す
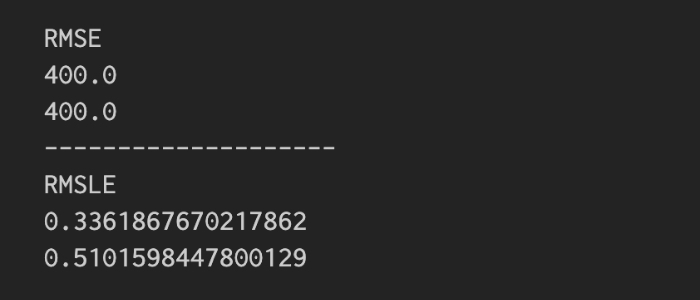
以下の結果からわかるように、RMSEでは予測値（y_pred_highとy_pred_low）が実際の値より大きく振れても小さく振れても誤差は同じになりますが、RMSLEは予測値が実際の値よりも小さい場合に値が大きくなる、つまり予測値が小さく振れた場合に大きくペナルティを課していることがわかります。
# ---データを準備
y_true = np.array([1000, 1000]) # 実際の値
y_pred_low = np.array([600, 600]) # 実際の値よりも予測値が小さい場合
y_pred_high = np.array([1400, 1400]) # 実際の値よりも予測値が大きい場合
# RMSE
print('RMSE')
print(rmse(y_true, y_pred_high))
print(rmse(y_true, y_pred_low))
print('-'*20)
# RMSLE
print('RMSLE')
print(rmsle(y_true, y_pred_high))
print(rmsle(y_true, y_pred_low))
RMSLEは小さなレンジの誤差に着目したいときに効果的
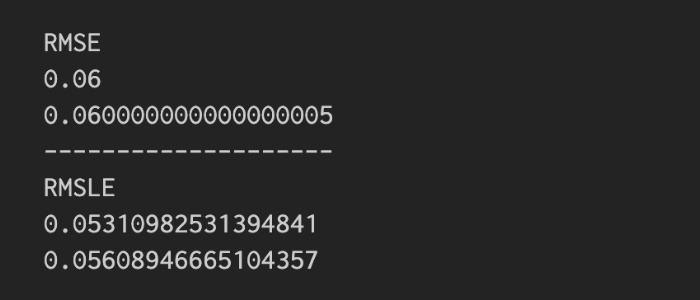
予測値と実測値の差が400の場合については上記で確認してきました。次は、以下のように予測値と実際の値の差が0.06である場合を見てみましょう。結果を見ると、RMSEよりもRMSLEの方が値の上下の振れによる違いを大きな値で表現していることがわかります。
# データを準備
y_true = np.array([0.1, 0.1]) # 実際の値
y_pred_low = np.array([0.04, 0.04]) # 実際の値よりも予測値が小さい場合
y_pred_high = np.array([0.16, 0.16]) # 実際の値よりも予測値が大きい場合
# RMSE
print('RMSE')
print(rmse(y_true, y_pred_high))
print(rmse(y_true, y_pred_low))
print('-'*20)
# RMSLE
print('RMSLE')
print(rmsle(y_true, y_pred_high))
print(rmsle(y_true, y_pred_low))
RMSLEは誤差が同じ場合は誤差の比率が大きい方に大きくペナルティを課す
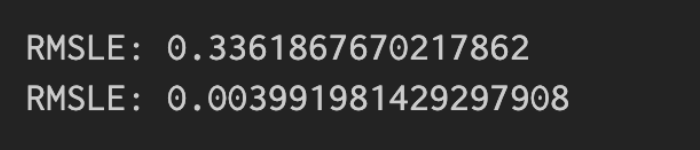
今度はRMSLEだけに注目し、予測値と実測値の差が同じでも実測値に対する誤差の比率が異なる場合の出力がどうなるかを確認してみましょう。RMSLEの二つの出力結果を確認してみると、実測値に対する誤差の比率が大きい方に対して大きくペナルティを課していることがわかります。
y_true = np.array([1000, 1000])
y_pred = np.array([1400, 1400])
print(f'RMSLE: {rmsle(y_true, y_pred)}')
y_true = np.array([100000, 100000])
y_pred = np.array([100400, 100400])
print(f'RMSLE: {rmsle(y_true, y_pred)}')
まとめ
さて、今回はRMSEとRMSLEという二つの性能評価指標それぞれの特徴を見比べながら理解を深めてきました。ざっくりとポイントを振り返ってみると、
概ねの回帰タスクに適しており大きな誤差に着目したい場合にはRMSEが適しており、実際よりも少なく予測してしまうことを避けたい場合やデータのレンジが大きい場合、実測値と予測値の誤差を比率や割合として表現したい場合などにはRMSLEが適しているとのことでした。
今回のRMSEとRMSLEのように、曖昧なまま何気なくこの指標を使っているなんていうことはやってしまいがちかもしれませんが、目の前の課題やタスクに応じて本当に適切な指標を選んで対処していけたらいいですよね！
今回はRMSEとRMSLEを中心に整理してきましたが、回帰タスクに使われる代表的な性能評価指標として他には決定係数R^2があります。こちらについても以前整理してみましたのでぜひこちらもご参考ください。
AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。
コメントをどうぞ