さよなら機械学習恐怖症！線形回帰と平均二乗誤差は友達 怖くないよ

「ボールはともだち こわくないよ」ならぬ「線形回帰と平均二乗誤差はともだち こわくないよ」なんて言えたら爽快ですよね。これらAI（機械学習）に関する専門的な単語を聞けば、普通は

「難しい話はマジで勘弁してください…」

なんて憂鬱な気分になるのが普通かもしれません。

※機械学習：AI（人工知能）を実現するための技術の一つで、近年非常に注目を浴びている。コンピュータがデータに潜むパターンや傾向を掴んで、そこから未知のデータの予測が可能になります

けれどAI（機械学習）について学んでいるとこうした単語にはよく出会いますし、ましてや仕事でAI（機械学習）を実装しようとするなら「知らないです」なんていうのはもってのほか。ただ「線形回帰」や「平均二乗誤差」は、コード数行を書けば動いて処理できてしまうこともあって中身の理解を後回しにしてしまうもの。。。（僕がそうでした）

これは例えるなら、車の製造会社が「仕組みはよくわかんないけど動くから売ってるんだよね」と言っているようなもの。そんな状態では今後この会社が発展していくイメージが全然持てませんし何だか気持ちが悪いです。

つっちー

こんな状態が今までの僕で、中身を詳しく理解せぬままきたとか、そうしたことが積み重なって実力不足で左遷＆今僕はこうして記事を書いているわけですが。

その時の話はこちら↓

僕が会社をクビになってもAIエンジニアを目指したその訳とは

AIエンジニアと言えば、今めちゃくちゃ花形な職業で、もしAI（人工知能）を自分で自由に作れるようになったら、そんな可能性溢れる姿にワクワクしますよね。「俺はAIエンジニアになる！」の思いつきから転職後、実力不足でいきなり左遷、それでもAIエンジニアになろうと僕の「最後の挑戦」が始まりました。

aizine.ai

そこで今回は機械学習アルゴリズムの基本である「線形回帰モデル」と非常に関係の深い「平均二乗誤差（Mean Squared Error：MSE）」について知識を整理していきます。

※機械学習アルゴリズム：データのパターンや傾向を数式で表現するモデルを構築するための一連の数学的な処理のこと

そもそも回帰とは？

知ったかぶりをしがちな僕なので一つずつ情報を整理しながらいきます（自分の癖ってなかなか直すのが大変ですよ 汗）。早速「線形回帰モデル」「平均二乗誤差」の内容に触れていきましょう！・・・の前に、まずは「回帰」の意味を念のため復習をしておきます。

以前（←詳しくはコチラ）整理したのですが機械学習のうち現在ビジネスで最も活用されている教師あり学習の一つに「回帰」がありました。いわゆる回帰分析というやつですね。
※教師あり学習：情報とその正しい判断（答え）をセットにしてコンピュータにデータのパターンを掴ませていく機械学習のこと

「回帰」とは、正解となる数値と入力データの組み合わせで学習し、未知のデータから売上や気温などの連続値を予測することでした。

その回帰のうちの一つが「線形回帰」です。

で、そもそも線形回帰って何よ？

という疑問が湧いてくるので、ここから「線形回帰」を理解し友達になるべく情報を整理していきます。（人も相手の理解を深めれば深めるほど友達になりやすくなりますよね）

愛の深さをテーマとした線形回帰モデル（通常最小二乗法）

何事も理解できないときはより具体的にわかりやすくして紐解いていくと解決の糸口が見えていくはずです！！線形回帰モデルってどんなん？ということを理解するために具体的な問題で考えてみます。

一番やさしい線形単回帰

例えば、自分が「愛の深さ研究家」だったとして、夫婦間における愛の深さをと結婚年数の関係を調べたいなあ・・・と考えたとしましょう。

様々な夫婦に聞き取り調査をしまくって次のような結果が得られたとします。こんな感じで・・・

A夫婦：結婚5年目、愛の深さは10よ！
B夫婦：結婚10年目、愛の深さは20よ！
C夫婦：結婚15年目、愛の深さは0だよ。もう愛なんてないよ。
D夫婦：・・・・・
・
・
・
（みなさん色々思うところや突っ込みたいところがあるかもしれませんがそこはご勘弁ください）

そして愛の深さとその夫婦の結婚年数の関係が次のようにグラフにプロット（図上に点をとること）できたとします。

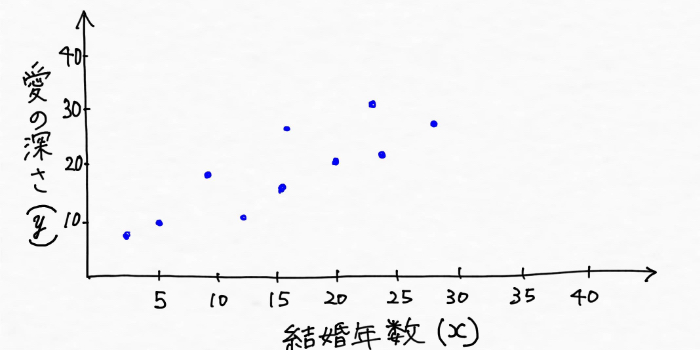
上手を見て「なんて素敵なんだ！！結婚年数が増えれば増えるほど愛の深さも増してるじゃないか！」と思われた方もいらっしゃることでしょう。

上図から愛の深さと結婚年数という二つのデータにはある一定の傾向、パターンがあることが見えてきたので、それらを上手い具合に表す線が次のように引けそうです。

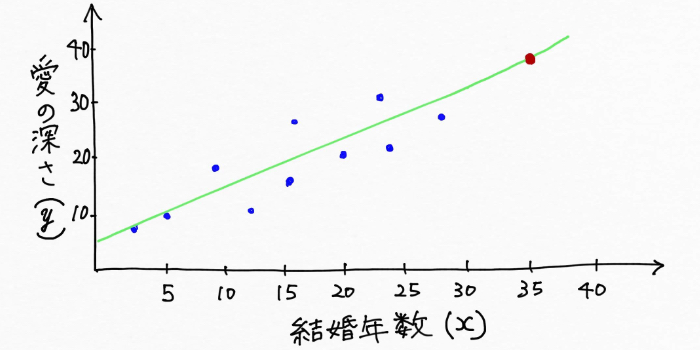
僕たち人間はこのような緑の線をチョチョイのチョイで書けてしまいますが実はこれはすごいことです！なぜなら、一度線を引いてしまえば聞き取り調査をしていない（結婚年数がわからない）夫婦についても直線から愛の深さを予測できるようになるからです。例えば聞き取り調査によるデータが無い結婚年数35年の夫婦の愛の深さ（上図での赤い点）も、緑の直線を利用すれば予測できますよね。

また、図上に線を引いたということはこれは数式で表現できるということです。このデータの傾向、パターンを表現しているこの直線の数式は一般的にモデルと呼ばれています。

機械学習の分野では求めたいものを「目的変数」、目的変数に作用する変数を「説明変数」と表現しますが、このとき求めたいもの（目的変数）である愛の深さをy、求めたいものに作用する（説明変数）結婚年数をxとすれば、

結婚年数x年のカップルの愛の深さは

y = w0　+　w1 × xで表現できそうです！

w0とw1にはそれぞれ何らかの一定の数字が入りますが、この数式こそが「線形回帰モデル」です！（だと理解しました！）

この例では「線形回帰モデル」は愛の深さ（目的変数）と結婚年数（説明変数）の関係を表現しており、図示すると先ほどの図のようにデータの傾向、パターンをつかんだ直線になります。聞き取り調査によって愛の深さyと結婚年数xがデータとして入手できるので、線形回帰モデルを構築するプロセスというのは、値がわからないw0とw1を手元にあるデータから見つけていくことだと言えます。

ちなみに、このように説明変数が1つだけの線形回帰は線形単回帰と呼ばれます。

キス回数、ハグ回数、感謝した回数など色々作用してくる線形重回帰

y = w0　+　w1 × xという式で結婚年数（説明変数）から愛の深さ（目的変数）を上手く予測できそうでしたが、冷静に考えてみれば

現実では結婚年数が増えれば増えるほど愛の深さが増すなんて、そんな単純なことはない！！愛はそんなに単純なものじゃ無いよ。

と思われた皆さんの声は最もなもので、実際もっと色んな要因が絡んでいますし人間関係はそんな単純ではありませんよね。なので、愛の深さ（目的変数）に作用する説明変数として「結婚年数」の他に「キスの回数」を加えさせてください。つまり、愛の深さには「結婚年数」と「キスの回数」という二つの説明変数が作用する場合です。

そしてまた、聞き取り調査をしたとします。この時先ほどの例と同じように聞き取り調査によってデータを集めたとしましょう。愛の深さ（目的変数）をyとして、説明変数である「結婚年数」をx、「キスの回数」をx1とすれば、今回の調査によるデータの傾向は、

y = w0　+　w1 × x　+　w2 × x1

と表現できそうです。w0、w1、w2にはそれぞれ何らかの一定の数字が入ります。

これは全て僕が理解をしやすいように例え話をして進めているので、実際愛の深さ（目的変数）に対して結婚年数（説明変数）が強く作用しているのか、キスの回数（説明変数）が強く作用しているのかはわかりません。

ただ、もし結婚年数（説明変数）xが愛の深さyに作用する影響が強いのなら結婚年数xの係数w1が大きくなり、逆にキスの回数（説明変数）x1による作用の影響が強いのならキスの回数x1の係数w2が大きくなるでしょう。

つまりw1やw2など説明変数の係数は、説明変数が目的変数に与える影響度合い、目的変数の値をつくる貢献度合いを表現するもので機械学習の分野では「重み」と呼ばれています。

つっちー

この「重み」という言葉について、以前は全然意味がわからなくて大変苦労しました。「重み」は英語では「Weight」と表現されます。Weightと聞くと「重量」という意味をイメージしてしまいますが、ここでの「重み」は「大切さや価値、重要性」の意味を持っています。

しかし、愛の深さ（目的変数）に作用するものとして「結婚年数」の他に「キスの回数」という説明変数を加えましたが、やっぱり

愛の深さはそんな単純に決まるものじゃ無いよ。

という声が聞こえてきます（というか僕も始めからそう思ってました）。。
冷静に考えてみれば実際には他にも「ありがとうを伝えた回数」、「心通わせた瞬間がどれだけあったか」・・・などなど終わりがありませんが、様々なものが愛の深さには関わっていますよね。

現実では例で上げたような一つ、二つの説明変数から目的変数を予測できる！なんていう単純な問題はほとんどないようで、目的変数を求めるためには様々な説明変数を考慮する必要があります！

このように実際はどれだけの説明変数（パラメータ）が関わってくるのかはわかりません。ただ、説明変数の個数がいくつになるかわからなくても線形回帰モデルの数式を一般的な形で表現できると便利です。

そこで説明変数がm個あるとして線形回帰モデルを表現すると、次のようになります。

y = w0 × x0　+　w1 × x1　+　w2 × x2　+・・・+　wm × xm

※x0＝1としてw0はy軸とモデルの交点（切片）を表しています

これが線形回帰モデルの数式です。（ようやく整理できました。）

また、このように求めたい目的変数が１つに対して、目的変数に作用する説明変数が複数個となる回帰分析のことを線形重回帰と呼びます。

適切なモデルを構築するためにはコスト関数を最小化すべし！

線形回帰について見てきたわけですが、、「じゃあどうやってコンピュータは適切な線を引く、つまり適切な重みを見つけてるの？」という疑問が出てきます。

人間だったらこんな風に簡単に線を引くことができるけれど、

コンピュータは一体どうやって線を引いとるんだよと。。。

そんな疑問を調べていって明快になったのは、線形回帰モデルを構築する際には、「構築したモデルがどれだけ悪いかを測定する関数」を利用して、この関数の値が最小になるようにして線を引いている！ということです。

ちなみに、「構築したモデルがどれだけ悪いかを測定する関数」を機械学習の分野ではコスト関数と呼ぶようで、「悪い度が小さければ小さいほど良くなる」という発想に基づいてコスト関数を小さくしていくことがモデル構築の際の肝となっているようです！

「平均二乗誤差（Mean Squared Error：MSE）」を理解すべく、一番わかりやすい直線で表される線形回帰モデルの場合を考えていくのですが、例えば次のようにデータがあった場合、

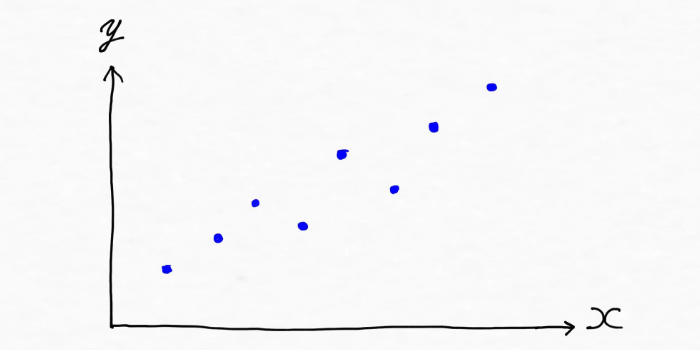
データの傾向を掴んだモデルを作る（線を引く）と、下記の緑線のような形になりそう。

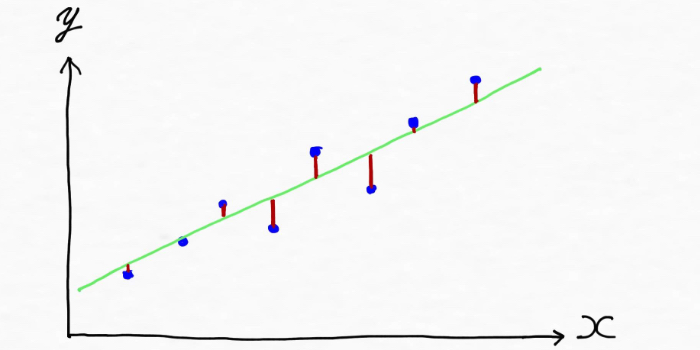
この時、実際の値とモデルによる予測値（緑線上の値）のズレ（誤差）は、上図では赤線部分（実際の値から作成した緑線に向かって縦線を引いた部分です）になります。

一方で次のようにデタラメな線を引いて仕舞えば、、、、

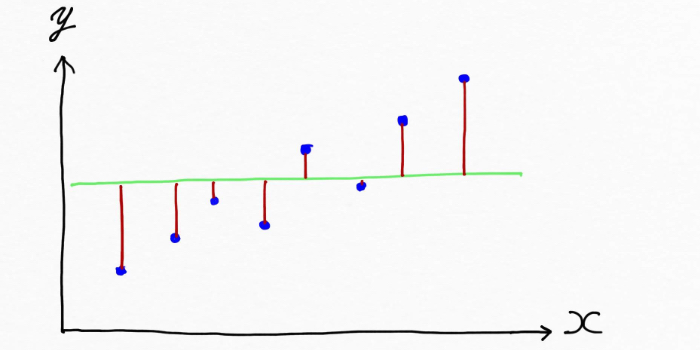
めちゃ赤線の長さが長い。。ああなるほど、実際の値とモデルによる予測値のズレ（誤差）が大きいということかあ。。となります。なので、この赤線の長さ、ズレを全体的に小さくできれば上手くデータの傾向を表現できるモデルになる！！ということが言えます。

つまり、コンピュータは、まず適当に線を引いて（モデルを作って）、手元にあるデータを元に実際の値とモデルによる予測値のズレ（誤差）という結果に基づいて、ズレ（誤差）が小さくなるように線の形を繰り返し調整していくことで適切な線の引き方を見つけていくというわけです。

平均二乗誤差（Mean Squared Error：MSE）は友達 怖くないよ

ここまで踏まえて、、、だったら赤線の長さの合計を求めてその平均が少なくなるようにすれば良いんだ！！

と僕は最初思ったのですが、そこには注意が必要でした。なぜならそのまま単に足し合わせてしまうと上図のように（実際の値 ー 予測値）が負の値をとる場合も出てきて、負の値が赤線（ズレ）の総和を打ち消して減らしてしまうことになるからです。

これではダメなので（実際の値ー予測値）を全て2乗することで値を全て正にした上で足し合わせをして、その合計の平均が一番少なくなる時が最適なモデルになる！とする手法を機械学習の分野では基本的に採用しています。

そしてズレがどれだけあるかを示すコスト関数（構築したモデルがどれだけ悪いかを測定する関数）が平均二乗誤差（MSE：Mean Square Error）です！適切な線形回帰モデルを構築するための指標とも言えるでしょう。

以上を踏まえて、実際の値とモデルによる予測値との誤差（ズレ）の2乗を足し合わせた平均値、つまり平均二乗誤差（MSE：Mean Square Error）は次のように表現できます。
※データが全部でn個あるとして「全部足し算するよ」の意味を持った記号であるΣ（シグマ）を用いています

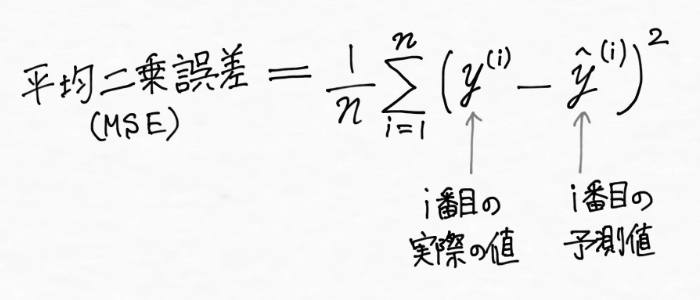
ここまで見てきたように線形回帰は平均二乗誤差（MSE：Mean Square Error）を小さくするようにモデルを訓練させていくので、通常最小二乗法（OLS：Ordinary least squares）とも呼ばれています。

平均二乗誤差平方根（RMSE：Root Mean Square Error）は友達 怖くないよ

さらにこの平均二乗誤差（MSE：Mean Square Error）の平方根をとったものを、平均二乗誤差平方根（RMSE：Root Mean Square Error）と呼びます。
※二乗平均平方根誤差と訳されることもあります

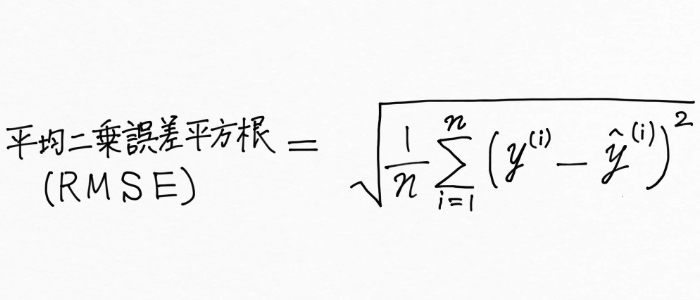
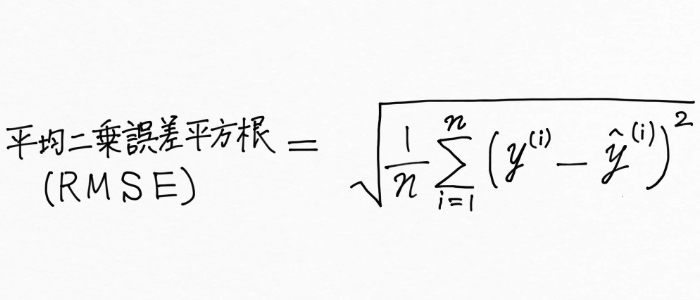
どんどん話がややこしくなっていくので、この平均二乗誤差平方根（RMSE：Root Mean Square Error）って何？ということを調べて整理したところ、これが回帰モデルの最も一般的な性能評価指標として用いられています。

平均二乗誤差平方根（RMSE：Root Mean Square Error）が最小になる時の重みが、データの傾向やパターンを上手く表現できるモデルの重みになるということですね。

ただ実際には平均二乗誤差平方根（RMSE：Root Mean Square Error）を最小にするよりも、平均二乗誤差（MSE：Mean Square Error）を最小にする方が簡単で計算しやすく結果も同じになる（関数を最小にする重みの値は、関数の平方根も最小にする）という理由で、モデルの構築に使われるのは平均二乗誤差（MSE：Mean Square Error）であることが多いようです。

つっちー

ちなみに、MSEとRMSEの使い分けについても調べて記事にしましたので、以下からご覧いただけます。

3分でRMSEとRMSLEをサクッと入門！特徴と使い分け方まとめ

RMSEやRMSLEは回帰タスクにおける代表的な性能評価指標ですが、これらが具体的にそれぞれどんな特徴があってどんな場面で使ったら良いのか？まで細かく説明できる人は案外少ないかもしれません。僕自身使い分けができなかったので、今回はこれら2つの評価指標について理解を深めることにしました。

aizine.ai

まとめ

さて、今回は思わず逃げ出したくなるような単語である「線形回帰」と「平均二乗誤差（MSE：Mean Square Error）」について整理をしながら理解を深めてきました。振り返ってみると、

ということを整理してきました。

つっちー

このコンテンツを書くまで線形回帰の評価指標は正解率じゃ無いの？って本気で思ってました 汗。こんな僕ですので、もしお気付きの点があった場合にはぜひ教えてください。

ここまできて、

「線形回帰と平均二乗誤差はともだち こわくないよ」

という状態になれたと思います（僕が）。

機械学習の分野のベースには数学があります。今回は少しだけ数式を用いたのですが、僕自身数学は決して得意な人ではなく、機械学習を学んでいて最初は数式に出会う度「ウッ」となっていました。

つっちー

大学で数学は学んでいませんし、高校時代には知らないうちに苦手意識を抱いていました。実際、機械学習の参考書を読む際にも数式が出てきたら飛ばして読んできたほど。

ただ、今回は情報を整理していきながら「わからない」が「わかる」になることの気持ち良さを改めて実感しましたし、何事も少しでもわかると面白くなったり一気に親近感が湧くものだということを強く感じました。今ではかつて自分が数学に対して抱いていたほど逃げ出したい感じはなくなっています。

よく私たちは一度挑戦してできなかったり、わからなかったりすると「自分に向いて無い」などと後ろ向きに考えがちかもしれません。ただ、そんな風に思うのではなくて例えば「この本は理解できないから違う情報源にあたってみよう」とかそんな風に気楽にやり方を変えてみる、別の角度から物事を眺めてみることが大事でしょう。

自分に能力が無いのではなくてやり方が悪いだけだと捉えて、行き詰まった時には一呼吸置いて別角度から眺めてみる。そんな習慣を身につけられたらもっと自分の可能性を開くチャンスが開くはずです。

＜参考＞

続く↓

機械学習の数学を避けてきた僕達が、今学ぶべきポイントと活かし方

AI（機械学習）を学んでいると「数学を学ぶべきだ！」という情報をよく耳にしますよね。ただ、「数学を理解せずともライブラリを使えば機械学習を回せるのになんでそんなに口酸っぱく数学数学って言うんですか？」というのが僕の心理です。そこで今回は具体的になぜ数学を学ぶべきで、どう活用していけるのかについてお伝えしていきます。

aizine.ai

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。