データ分析業務や統計、機械学習に携わり始めると「決定係数」や「Ｒ2」「アールツースコア」「寄与率」などの用語を見聞きして「これ何？」と頭を悩ませた経験は誰にでもありますよね。これらは全て同じものを意味していますが、これなんだろう？と思いググって見るものの、小難しい数式や説明で「ああ、もう嫌・・・」なんて憂鬱な気分になる方は多いかもしれません。
実際僕がそうだったのでそうした気持ちはよくわかります。しかも、
なんてこった・・・簡単に理解しやすそうなページが全然見つからない_:(´ཀ`」 ∠):
このままでは僕と同じように憂鬱な気分になる人が今後も出続けるに違いないし、統計や機械学習を理解していく一つの障壁になっていることは間違いない・・・。だったらわかりやすく整理したら助かる人が絶対いるし、僕も勉強になって一石二鳥だよね！！僕はそう思いました！
そこで今回は決定係数（Ｒ2）について整理をすることにしました！読んだ後には決定係数（Ｒ2）とは何で、何を意味するものでどう見たらいいのかがイメージできるようになっているはずです（頑張って整理していきます！！）。
※決定係数は数式でＲ2と表現されます。
決定係数（Ｒ2）その前に「回帰」とは
早速決定係数（Ｒ2）にふれていくのですが、理解を深めるためには「回帰」という言葉を先に押さえておく必要があります。そこでまず「回帰」の意味から整理していきましょう。
回帰を既に理解されている方は本章は読み飛ばしてください
この回帰という言葉、調べて見るといろんな言葉で表現されており、統計の分野から見たときの説明と、機械学習の分野から見たときの説明では少し表現が違っているように見受けられたので念のため両方記載しておきます。ただ本質的には同じものを指しています。
※機械学習：AI（人工知能）を実現するための技術の一つで、近年非常に注目を浴びている。コンピュータがデータに潜むパターンや傾向を掴んで、そこから未知のデータの予測が可能になります
統計から見た「回帰」
回帰とは、求めたいものが売上や気温などの連続値であるときに、データの傾向やパターンを表現する数式を当てはめることです。
機械学習から見た「回帰」
「回帰」とは、正解となる数値と入力データの組み合わせでデータに潜むパターンや傾向を見つけ、手元に無い未知のデータから売上や気温などの連続値を予測することです。
（回帰についてもっと詳しく理解したい方はこちら↓）
決定係数（Ｒ2）とは
本章からいよいよ決定係数（Ｒ2）について触れていきます！
回帰によって求めたデータの傾向やパターンを表す数式（例えばy＝ax+bのような）のことをモデルと呼びます。
そして今回のテーマである決定係数（Ｒ2）とは、
回帰によって導いたモデルの当てはまりの良さを表現する値で、モデルによって予測した値が実際の値とどの程度一致しているかを表現する評価指標です。
これは言葉だけでは理解しづらいので図を見てみましょう。例えば、次の図では青の点で示されているデータに対して、データの傾向、パターンを表す線が引かれています。この線がモデル（緑色）です。
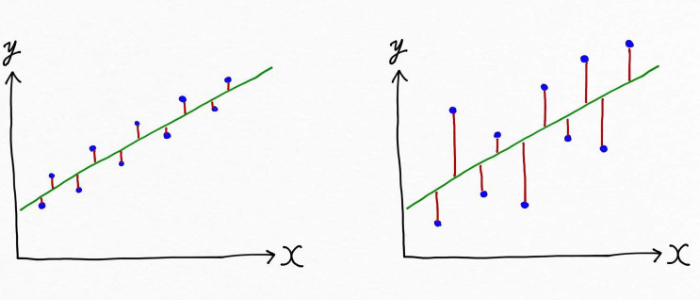
赤の縦線はデータの実際の値とモデルが導いた（予測した）値のズレ（誤差）を示しています。左図はズレ（誤差）が小さいですが、右図は左図よりもズレが大きいことがわかりますよね。これはつまり、左図のモデルの方がより適切にデータを表現できている！ということです。
こうしたモデルによる予測が実際の値に比べてどのくらい当たっているのか（どれだけズレが小さいか）を客観的に示す指標が決定係数（Ｒ2）です。
決定係数（Ｒ2）は普通０〜１の範囲の値をとり、値が大きいほどモデルが適切にデータを表現できている（線を引けている）ことを意味し、小さいほど適切にデータを表現できていないことを意味します。
具体的にはモデルの予測値と実際の値のズレ（誤差）が小さいほど決定係数（Ｒ2）は１に近づき、１では完全に一致（引いた線（モデル）の上に完全にデータが乗っている）しします。逆に予測値と実際の値のズレ（誤差）が大きいほど決定係数（Ｒ2）は小さくなり、予測が当たっていない状態を示します。なので決定係数（Ｒ2）の大小からモデルの良し悪しを判断できるというわけです。
※決定係数（Ｒ2）が負の値をとる場合も時にありますが、そのような時はわざと予測を外すモデルになっていると判断できます。
決定係数（Ｒ2）は説明変数が目的変数をどれくらい説明できるかを表す
決定係数（Ｒ2）の説明を調べていると、「決定係数（Ｒ2）は説明変数（独立変数）が目的変数（従属変数）をどれくらい説明できるかを表す値です」なんていう難しい説明も見られます。
これはどういうことかと言うと、機械学習や統計の分野では
- 求めたいものを目的変数（従属変数）
- 求めたいものに作用する変数を説明変数（独立変数）
と表現します。
例えばy=ax+b（直線になりますね！）という数式でデータの傾向を表現するモデルがあった場合、求めたいもの（目的変数）はy、目的変数に作用するものは説明変数xです。この時モデルはy＝ax+bなので、説明変数xの値は目的変数yの値を決定する＝説明することになると言えますよね。
データの傾向、パターンを上手く捉えられたモデルであればあるほど、モデルによって実際の値に近いyをxで説明できます。なので、「決定係数は、説明変数（独立変数）x が目的変数（従属変数）y をどれくらい説明できるかを表す値です」と言われているんですね。
サイコロの目を6分の1で予測→Ｒ2＝0、100％的中→Ｒ2＝1
また、別の角度から見てみると、決定係数（Ｒ2値）は常に平均値を出力する回帰モデルに比べて、相対的にどのくらい性能が良いかを表しているとも言えます。難しい表現ですが、これはサイコロを例に考えてみましょう。
サイコロをころころと転がした場合、各目が出る確率は6分の1ですよね。サイコロをふって出る目が何かを予測しようとした場合、モデルによる予測精度が6分の１なら決定係数（Ｒ2）は０になり、次に出る目を完全に予測できる時には決定係数（Ｒ2）は１となります。
つまり決定係数（Ｒ2）は、自然に起こる確率よりもどれだけ高い確率でモデルが結果を導けているか、ということがわかる指標とも言えます。
ここまで様々決定係数（Ｒ2）について見てきましたが、回帰モデルを評価するには決定係数（Ｒ2）が最も直感的な基準だと言われています。
決定係数（Ｒ2）の値をどう判断するか
決定係数（Ｒ2）は普通０〜１の範囲の値をとることは前述しました。
データサイエンティストとして現在活躍されている方から僕が以前直接聞いた話ですが、決定係数（Ｒ2）を判断する大体の目安としては下記があるようです。（ただ人によって様々な見方があります）
この過学習というのは、モデルが「学習に使ったデータに対してはきちんと予測できるけど、知らないデータに対しては全然当たらない」という実用性を全く伴っていない状態のことです。（過学習についてもっと知りたい方はこちら↓）
ただ、もちろん過学習には陥っておらず未知のデータにも対応できるモデルの状態で決定係数が非常に高いという場合もあります。そのような場合はデータが非常に綺麗であること、つまり説明変数（パラメーター）に目的変数を説明するための十分な情報量があったことが考えられるでしょう。
＜参考＞決定係数（Ｒ2）の数式
決定係数は一般的には以下のような数式で表現されます。
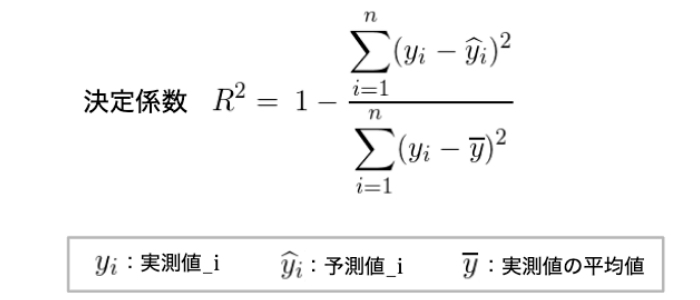
※決定係数の数式が以下のように間違っておりましたので2019年11月25日に修正いたしました。
誤 1- Sum_i (予測値_i – 実測値_i)^2 / Sum_i(予測値_i – 実測値の平均値)^2
回帰モデルの評価をする際、決定係数（Ｒ2）だけを見ていてはいけない
回帰モデルの評価する際には、決定係数だけを見て判断していてはいけません。決定係数（Ｒ2）の値を見るだけでなく、モデルそのものの汎化性能を見る必要があります。なぜなら前述したように決定係数（Ｒ2）が高くても未知のデータに対する予測が低ければ、それは汎化性能があるとは言えず過学習に陥っていることになるからです。決定係数（Ｒ2）は平均二乗誤差（MSE）の尺度を取り直した一つの姿です。R2値＝１のとき、モデルはMSE＝０で完全に適合することになります。
自由度調整済み決定係数
決定係数（Ｒ2）とは別に「自由度調整済み決定係数」というものもあり、中には聞いたことのある方もいるかもしれません。
こちらは決定係数（Ｒ2）が説明変数（独立変数）の数が多くなるにつれて大きくなるという欠点を補うためのものです。自由度とはパラメータと思えばわかりやすいでしょう。説明変数（独立変数）の数で調整した決定係数（Ｒ2）を、自由度調整済み決定係数と呼びます。
まだ理解しづらいので具体例で考えていきましょう。
例えば「道端で出会った500組の夫婦に聞き取り調査を行った」とします。聞き取り調査によって得られたデータを利用して愛の深さを予測できる回帰モデルを作成し、その回帰モデルを利用して決定係数（Ｒ2）を算出したとします。
ここで冷静に考えてみると、作成した回帰モデルはあくまで「たまたま道端で出会った夫婦500組」に対して予測が当たるように作られたものですよね。この作成したモデルを、仮に国内全ての夫婦を対象として利用してみたとすれば予測結果は悪くなるでしょう。なぜなら、500組のデータの傾向と国内全ての夫婦データのそれは異なるはずからです。
そのため、500組の夫婦の聞き取りデータから導いたモデルの決定係数（Ｒ2）を国内全ての夫婦を対象としたものとして考えようとすれば、モデルによる予測の当てはまりの良さを本来よりも高く評価していることになってしまいます。
こうした問題が起こるので、あくまで「国内全体を対象」としたモデルの評価を見積れるように決定係数の値に調整を加えたものが「自由度調整済み決定係数」です。決定係数の値を修正するのにデータ数と説明変数の個数から求められる「自由度」という数字を用いているため「自由度調整済み決定係数」と呼ばれているんですね。
まとめ
さて、今回は頭を悩ませがちな決定係数（Ｒ2）について一つずつ整理してきました。
- 決定係数（Ｒ2）とは、回帰によって導いたモデルの当てはまりの良さを表現する値で、モデルによって予測した値が実際の値とどの程度一致しているかを判断する評価指標である
- 決定係数（Ｒ2）は値が大きければ大きいほど良いが決定係数だけでなくモデルそのものの汎化性能を見る必要がある
- 決定係数と自由度調整済み決定係数がわかる場合は、後者を利用すると良い
といったことを中心に見てきましたよね。
決定係数（Ｒ2）をはじめとして、専門用語は小難しい印象を与えるものばかりです。そうした背景もあって統計や機械学習の世界に足を踏み入れることに、最初は中々ハードルが高いと感じてしまう人も多いかもしれません。しかし一つ一つを紐解いていけば、わからない苦痛がわかる喜びへ、わかるが興味へ、そして面白さへと変わっていくものでしょう。
僕は囲碁AIに興味を持ったことをきっかけに機械学習に興味を持ちました。学びを深めているうちに自然と機械学習に関連が深い数学や統計学を学ぶことがどんどん面白くなっています。学生時代にこれらが苦手だったにも関わらず。。。
意味のわからない単語や考えに出会ってつまづいた時には誰しも憂鬱な気持ちになるものですが、何が今わからないのかを一つ一つ紐解きながら、ゆっくりとでも自分のペースで学びを深めていきたいものですよね！その繰り返しの先にきっと楽しい状況が待っているでしょう。
＜参考＞
AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。
コメントをどうぞ
一般的に相関係数が0.6あれば、相関があるとされます。
一部医療系では0.7を基準にしてる所もあります。
寄与率は二乗になる為各々、0.36、0.49になります。
以下記載は相関と寄与率の間違いと思うので確認お願いします
＜決定係数（Ｒ2値）の判断目安＞
0.6以下：モデルとして意味なしていない（全然予測できてない）
0.8以上：すごい良いモデルができた！よくやりました！※ただ0.8以下の数値であってもデータ同士の関連性が存在する場合もあるので一つの指標としてみるべき。
0.9以上：大丈夫？過学習してないか？
とても勉強になりました。
私もPLS回帰分析を使用して、アンケートなどの主観的な項目から、その方の日常生活レベルを予想可能なモデルを作成できるか試みていますが、Q2およびR2の決定係数をいくつに設定しなければいけないか、悩んでいます。インターネットにはR2は0.5以上と記載されていましたが、引用できる論文や書籍があれば教えて頂きたいのですが、いかがでしょうか？
非常に説明がうまいですね！
分かったような気になりました。
ほかのどのサイトよりも一番わかりやすかったです！
論文を読んでいてR2乗が出てきて困っていたのですがとても分かりやすく助かりました！
たつさん、こちらこそ読んで頂きありがとうございます。お役に立てたようで、一生懸命記事を書いた僕としても大変嬉しいです！
凄く分かりやすい説明で参考になりました！
１つ質問させて下さい。
統計ソフトJMPでロジスティック回帰分析を行っているのですが、各パラメータ(説明変数)のR2乗はどうすれば求めることができるでしょうか。
よろしくお願いいたします。
統計初心者さん、ありがとうございます。
決定係数が意味するのは「説明変数が目的変数をどれくらい説明できているか」つまり「モデルの適合がどれだけ良いか」ですので、各パラメータ(説明変数)のR2乗という表現はしないと思います。
各パラメータ（説明変数）の重要度を求めたい？（認識が間違ってましたらごめんなさい）ということを仰っているのでしたら、ランダムフォレストなどを利用すればできますので是非調べてみてください(^^)
わかりやすい例などが多く参考になりました。
いくつか質問させていただきたくコメントいたします。
・R2が高すぎる場合の過学習というのはあまりにも一致しすぎており、もしかしたら他の未知の変数を投入したらまったく異なる値になる危険性があるような状態なのでしょうか。他ページも見させていただきましたが、評価指標としてMSEがあるとのことですが、MSEが低すぎる場合でも同じように過学習になっている可能性があるかと思うのですが、過学習になっている不適切なモデルか十分に考慮されて素晴らしいモデルかという判断はどのような観点から行えるのでしょうか
・サイコロの例ですが、出る値が100%予測できるものがR2＝1となるのは理解できましたが予測精度が1/6の場合はなぜR2＝0となるのでしょうか。
単純に予測の精度が1/6のため1/6=16.6%程度の適合性はあるのではないかと考えてしまったのですが。
統計の勉強が不十分であり申し訳ありませんがご教示いただけると幸いです。
かつおさん
こちらこそ、記事を読んでくださってありがとうございます！
質問頂いた件についです。返信遅くなり申し訳ないです。
＞・R2が高すぎる場合の過学習というのはあまりにも一致しすぎており、もしかしたら他の未知の変数を投入したらまったく異なる値になる危険性があるような状態なのでしょうか。
→→過学習は学習済みのデータに対しては適合しているけれど、未知のデータに対しては適合しておらず予測が全然できない状態です。過学習については視覚的にイメージできると理解が深まると思いますし、以前記事も書いておりますので、よければこちらをご覧ください。
https://aizine.ai/overfitting0206/
＞他ページも見させていただきましたが、評価指標としてMSEがあるとのことですが、MSEが低すぎる場合でも同じように過学習になっている可能性があるかと思うのですが、過学習になっている不適切なモデルか十分に考慮されて素晴らしいモデルかという判断はどのような観点から行えるのでしょうか
→→学習データに対する予測精度と、未知のデータに対する予測精度を比べてみた時に、差がある場合は過学習していると判断できます。学習データに対する精度は高いけれど、未知のデータに対する精度が低いというような状況です。素晴らしいモデルになっているかどうかというのは、プロジェクトごとに設定した基準値をクリアしているかどうかで判断すれば良いと思われます。データ分析やモデル構築を通じてビジネスの課題を解決することが一番大事な目的ですので（ちなみに私はエンジニアではなく実務未経験ですが 汗）。
＞サイコロの例ですが、出る値が100%予測できるものがR2＝1となるのは理解できましたが予測精度が1/6の場合はなぜR2＝0となるのでしょうか。単純に予測の精度が1/6のため1/6=16.6%程度の適合性はあるのではないかと考えてしまったのですが。
→→決定係数は、説明変数が目的変数をどれくらい説明できるかを表す値です。ご存知の通り、サイコロは理論上6分の1の確率でいずれかの目が出ます。つまり、6分の1の確率で出る目を言い当てるというのは、ランダムに１〜6の数字を言うのと同じ ＝ 「全く予測をしていない」と言い換えられます。そのためR^2＝0となります。
私もまだまだ勉強中でして数式で計算した値が一致しない理由はわからないのですが、今回決定係数を求める数式は主に以下の2冊を参考にさせて頂きました。
・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.
・『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』
もし興味があれば、ぜひ参考にしてみてください。
このサイトに掲載されている決定係数の式の除算項の分母が
（予測値ー実測値の平均）^2
とあります。しかし，決定係数には複数の定義がありますが，ここで実測値の平均を用いることは自分の知る限りありません。決定係数は「実測値のばらつきに対し，どこまで小さい分散で予測できたか」であると考えられます。従って，分母は実測値のばらつきを表す
（予測値ー予測値の平均）^2
であると思います。
決定係数の複数の定義に関しては以下を参考にしました。
Kvålseth, T. O. (1985). Cautionary note about R 2. The American Statistician, 39(4), 279-285.
https://www.tandfonline.com/doi/abs/10.1080/00031305.1985.10479448
きっしーさん、ご指摘ありがとうございます。私自身、決定係数についてまだまだ完全に理解できているという訳ではないため、本記事では以下の書籍の情報を参考にしながら数式を紹介させて頂きました。
・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.
・『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』
私自身勉強中なため、これが正しい、これは誤っているという正確な返信はまだまだできないのですが、このような形でコメントをくださることで私含め本ページを訪れてくださった皆様の理解も一層深まりますので、大変感謝しています。ありがとうございます。
To: きっしーさん
> 分母は実測値のばらつきを表す
> （予測値ー予測値の平均）^2
> であると思います。
上記は
（実測値ー実測値の平均）^2
の誤記では？
To: つっちーさん
分母は、
Σ（実測値ー実測値の平均）^2
が
コメントにリンクしてあるsklearnの定義には合いますね。
『v is the total sum of squares ((y_true – y_true.mean()) ** 2).sum()』
しかし、参考にされた書籍だと、
Σ（予測値ー実測値の平均）^2
と記載されているのですかね？
「記事有難うございます。」さん、改めて以下の書籍の該当箇所を確認したのですが、Σ（予測値ー実測値の平均）^2 となっておりました。
・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン. p74
To: つっちーさん
ご返信有難うございます！
決定係数ですが、コメントできっしーさんが述べられているように私も下記のイメージを持っております。
> 決定係数は「実測値のばらつきに対し，どこまで小さい分散で予測できたか」であると考えられます。
しかし書籍の記載が正しいとするとイメージと合わないため、書籍の正誤表を調べてみたところ
決定係数の定義に修正が入っておりました。
正誤表はgithubの下記レポジトリのwikiで公開されているためご参考にして頂ければと思います。
・ oreilly-japan/ml-at-work
・ 正誤表：3.2.2 決定係数 p74一番下の数式右辺
「記事ありがとうございます。」さん、教えてくださりありがとうございます。正誤表確認いたしました。
「記事ありがとうございます。」さん、「きっしー」さん、がご指摘くださった通り、決定係数の数式の分母は正しくは、
Σ（実測値ー実測値の平均）^2 でした。
大変勉強になりましたし、本ページの内容も修正いたします。誠にありがとうございました！
決定係数を求めるの数式が、他のサイトで掲載されている数式と全然違うと思ったのですが、気のせいでしょうか。
pythonのscoreで出した決定係数と、このサイトに掲載されている数式で計算した決定係数を比較したのですが、まったく合わず。。
決定係数を求める数式は一つだけではないので、採用している計算式によって出力が異なります。例えば、scikit learnの線形回帰の決定係数（socore関数で出力される値）は、こちらのページで掲載されている定義と同じようですね。
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
匿名希望その２さん、なるほどそういうことだったんですね！！コメントありがとうございます。