AI(機械学習)の勉強をしていると「ロジスティック回帰」というアルゴリズムはじゃんじゃん出てきてよく目にしますよね。便利なご時世ですからライブラリという魔法のツールを使えば、僕たちはこのロジスティック回帰の中身を理解していなくても正直使えちゃうわけです。
目的を達成できればそれで言い訳ですが、やっぱり中身のよくわからないものを使うのには気持ち悪さを覚える人もいることでしょう。実際僕がその一人な訳で「そろそろ中身をちゃんと理解しておこう」と思ったので今回はこのロジスティック回帰について「基本のき」から調べて整理してみることにしました。
そもそもロジスティック回帰とは何なのか?


まず、ロジスティック回帰は教師あり学習(※)の分類タスクに用いられるシンプルで最も一般的な線形クラス分類アルゴリズムの一つで、そのシンプルさゆえに最初に試す分類器として適しているということで広く用いられています。
ロジスティック回帰は、名前に「回帰」と入っていますが、実際には分類タスクに適用される分類アルゴリズムなので注意が必要です。


僕は昔名前に騙されてましたので、もしご存知なかった方は僕みたいに間違えないようにご注意ください(^^)
※教師あり学習:機械学習のうちの手法の一つ。
※クラス:機械学習の分野では、分類対象のカテゴリのことをクラスと言います
ロジスティック回帰の3つの特徴


全体像を掴む意味でも、まずはロジスティック回帰の代表的な特徴についてまとめてみました。
出力とは別に、その出力のクラスに所属する確率値が出せる
ロジスティック回帰はある事象が起こる確率を予測、分析したい時に用いられるもので、分類が曖昧なものを判別することが得意と言われていて、データが各クラスに所属する確率を計算することで分類を行います。
例えば、自分が雪国に住んでいるとして、もし明日雪が降るようならタイツを二枚重ねで履いて外出する、もし雪が降らなければタイツは1枚にすると考えていたしましょう。今の気温が1℃だった時、明日雪が降らずにタイツ1枚で外出できる確率はどれくらいかを知りたいとします。
こんな場面でロジスティック回帰を使うと、明日はタイツ1枚なのか2枚なのか、そしてそれぞれの確率を求めることができるんです。


このように二つに分けるケースは二値分類や2クラス分類と言いますが、ロジスティック回帰は三種類以上の分類問題にも利用することができます。
学習はオンライン学習でもバッチ学習でも可能
そもそもオンライン学習とバッチ学習って何やねん?となったので(僕が)最初に整理しますが、どちらも機械学習モデルの学習を行う方法のことを言い、どのような方法で最適なモデルを構築するかという最適化(重みを計算)の方針が異なっています。
まずオンライン学習は、データを一つずつ読み込んでその都度モデルの更新を繰り返すことで学習を行う手法です。一方でバッチ学習とは、モデルの最適化(最適な重みを見つける)のために一度に全てのデータを読み込んでから学習を行う手法です。
現在世間を賑わしているディープラーニングではオンライン学習が必須となっていますが、ロジスティック回帰ではどちらの方法でも学習が可能なんですね。
予測性能はまずまず、学習速度は早い
ロジスティック回帰はシンプルな線形分類器で、そのシンプルさゆえに最初に試す分類器として適しています。パラメータ数もそれほど多くなく予測に時間がかからないこともあり、様々な機械学習アルゴリズムを比較する際のベースライン(基準となる比較対象)としてよく使われています。分類タスクの場合には、とりあえず最初はロジスティック回帰を使ってみよう、という考え方でもいいのかもしれません・・・。
ロジスティック回帰の仕組み


ロジスティック回帰では、あるデータポイントx(特徴量からなるベクトル)とそれが属するクラスを表すラベルyから学習を行い確率を計算します。少しわかりづらいので前述のタイツの例で整理してみましょう。
今の気温から明日雪が降るかどうかでタイツを1枚履くのか2枚履くのかを予測するケースならば、
- 雪が降らずタイツが一枚の場合に「0」というラベルをつける
- 雪が降ってタイツが二枚の場合を「1」というラベルをつける
とすれば、0と1で場合を分けて表現できますよね。
ロジスティック回帰を使って、今の気温(x)からタイツが1枚か(y=0)、タイツが2枚か(y=1)を確率で求められるということです。確率なので、例えば今の気温が2℃のとき、明日雪が降らずにタイツが1枚である確率が80%、雪が降ってタイツが2枚である確率は20% というように表現されます。
ロジスティック回帰の基本的な仕組みは、次の線形回帰の数式と同じように、データx(特徴量からなるベクトル)に対して重みベクトルw(w1, w2, …wm)をかけてバイアスw0を加えたyという量を計算します。
y = w0 × x0 + w1 × x1 + w2 × x2 +・・・+ wm × xm
※線形回帰について詳しく知りたい方はコチラ
また、重みとバイアスをデータから学習する点も線形回帰と同じです。ロジスティック回帰が線形回帰と大きく異なっているのは、ロジスティック回帰では確率を計算するために出力の範囲を0〜1にするために「シグモイド関数」というものを用いていることです。順番に整理していきましょう。
シグモイド関数とは次のようなグラフで、与えられた数字を0から1の範囲に変換します。
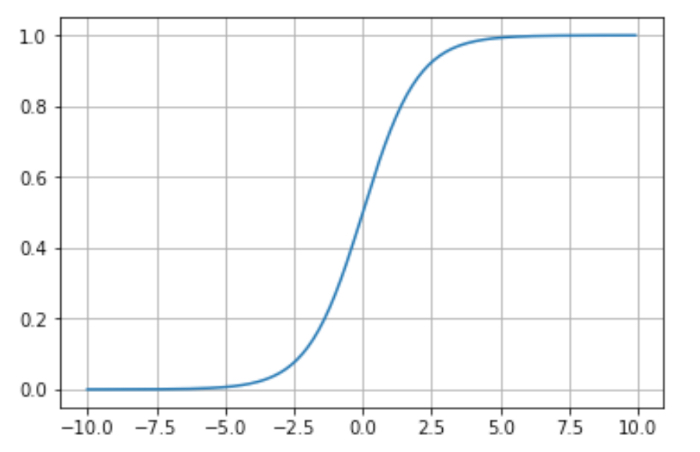

グラフからわかるように、シグモイド関数には入力が0の時は0.5をとり、値が小さくなるほど0に、大きくなるほど1に近くなる性質があります。こんな緩やかなカーブを描くシグモイド関数は次の数式で表現されます。
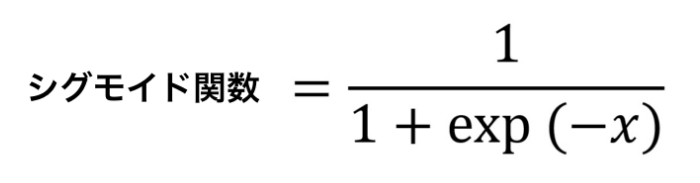
※expはネイピア数とよばれる2.718‥‥という数字
ちなみにシグモイド関数を一般化したものはロジスティック関数と呼ばれており、ロジスティック回帰の由来となっているようですね。そしてロジスティック回帰は、
線形回帰の数式(y = w0 × x0 + w1 × x1 + w2 × x2 +・・・+ wm × xm)が、
シグモイド関数 1 / 1+exp(-x) の中に組み込まれている形で表現されます。
つまり線形回帰の数式を z = w0 × x0 + w1 × x1 + w2 × x2 +・・・+ wm × xm
とすれば、確率を表すロジスティック回帰はシグモイド関数 1 / 1+exp(-x) を用いて、
あるデータXが与えられたときにラベルyが、 y=1 になる確率Pはを数式で表現すると、
P(yi = 1 | X)= 1 / 1 + exp(-z) となります。
ロジスティック回帰はシグモイド関数の出力があるクラスに属する確率になり、タイツを1枚にするか2枚にするか、のような2つのケースで分けられる二値分類の場合、通常は0.5より大きいかどうかでどちらのクラスに分類されるかを予測します。
損失関数は交差エントロピー誤差関数と呼ばれるものである


さて、「構築したモデルがどれだけ悪いかを測定する関数」を機械学習の分野ではコスト関数と呼び、このコスト関数を小さくしていくことが一般的にモデル構築の肝となっています。ご存知の方も多いことでしょう。ロジスティック回帰のコスト関数は交差エントロピー誤差関数と呼ばれていて、他の誤差関数同様に分類に失敗すると大きな値をとり、分類に成功すると小さな値をとります。
この交差エントロピー誤差関数は、N個のデータに対してyを出力、tを正解ラベル(正しい場合は1、間違っている場合は0とする)、logを底がeの自然対数とすると、次の数式で表すことができるようです。
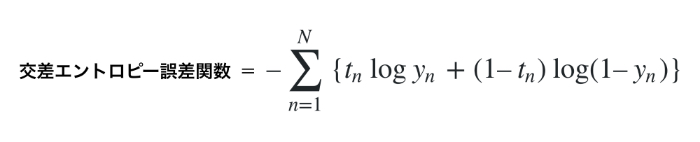
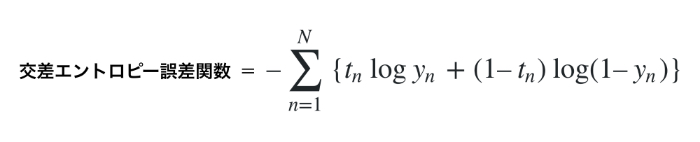
なにやらごにょごにょして複雑な数式に見えるのですが、冷静に見つめてみると意外にそんなこともないかもしれません。正解(t=1)の時はlogynを考えればよく、不正解(t=0)の時は、log(1-yn)を考えればよいことになります。
計算してみるとわかるのですが、重みと入力の積和(前述の例でいう線形回帰の数式(z) )が0より小さい損失が急激に大きくなり、0より大きいと段々小さくなっていくんですね。
パラメータCを大きくすると正則化は弱くなる


ロジスティック回帰には、過学習を防ぐための正則化項があります。正則化とは、過学習を防いで汎化性能(未知のデータへの対応能力)を高めるためのテクニックの一つで、モデルに「正則化項」というものを付けることでモデルの形が複雑になりすぎないように調整しようとするものです。
ロジスティック回帰における正則化の強度を決定するパラメータはCと呼ばれ、Cが大きくなると正則化は弱くなります。つまり、パラメータCを大きくするとロジスティック回帰は訓練データに対しての適合度を上げようとし(個々のデータポイントを正確にクラス分類することを重視するようになる)、逆にパラメータCを小さくすると係数ベクトルwを0に近づけることを重視するようになります(適合度を下げて大雑把にデータの傾向をつかもうとする)。
※過学習:学習データに対してはきちんと正解できるけど、未知のデータに対しては全然当たらないモデルの状態のこと。詳しく知りたい方はコチラ
まとめ


さて、今回はロジスティック回帰について整理してきました。整理してきたことを振り返ってみると、
- ロジスティック回帰は出力とその出力のクラスに所属する確率値を確認できる
- 学習はオンライン学習でもバッチ学習でもできる
- 予測性能はまずまずで学習速度は早い
- 損失関数は交差エントロピー誤差関数である
- ロジスティック回帰は線形回帰の数式がシグモイド関数の中に組み込まれている形で表現される
- パラメータCを大きくすると正則化は弱くなる
ということでした。ロジスティック回帰は実は産業界において最も広く使用されている分類のアルゴリズムの1つです。例えば気象予報において雨がふるかどうかだけでなく、降水確率も発表するために使われていたり、特定の症状に基づいて患者が疾患にかかっている確率を予測する、広告のクリック予測など、様々な分野で広く利用されています。
ロジスティック回帰を生み出してくださった先人たちに感謝しながら、引き続き自分の目的に合わせて必要に応じてロジスティック回帰を活用していきたいですね!


AI(人工知能)って「なにそれ美味しいの?」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください(実話)。
<参考>
・秋庭 伸也 (著), 杉山 阿聖 (著), 寺田 学 (著), 加藤 公一 (監修) (2019)『見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑』.翔泳社







コメントをどうぞ
ネイピア数はexpではなくeかと
丁寧に説明して頂いているのに、依然むつかしく感じるのは、私だけでしょうね(辛)
ロジスティック回帰まだ分からない、利用方法実例がもう少し現実味有る例があれば少し近づけるかも
ぎんやんま係さん
ロジスティック回帰難しいですよね。今回僕の説明例もおかしかったかもしれません 汗
ロジスティック回帰の説明は、個人的には書籍『見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑』が一番わかりやすく、数式で理解を深めたい場合は『やさしく学ぶ 機械学習を理解するための数学のきほん』がわかりやすかったです。
もし興味あればぜひ参考にしてみてください。