交差検証（cross validation／クロスバリデーション）の種類を整理してみた

機械学習を学んでいると、交差検証（cross validation／クロスバリデーション）というワードをよく見かけます。このご時世、便利なツールであるライブラリがたくさん公開されていて、交差検証もコード数行で利用できてしまう超便利な状況ですから、ざっくりとした理解で済ませている方は意外に多いのかもしれません。

実際僕自身が、

つっちー

「交差検証って過学習を防いで汎化性能を高めるためにデータを分割するアレだよねアレ！」

的な感じで理解していたのですが、機械学習の勉強を進めれば進めるほどに、そうした曖昧な理解ではとうとう困る場面がチラホラ出てきました。交差検証（cross validation／クロスバリデーション）には様々な種類があるので「とりあえず単純な交差検証でOK！」というやり方では痛い目を見る訳です。

そこで今回は交差検証（cross validation／クロスバリデーション）について整理することで学びを深めることにしました。（すでに現場でバリバリ活躍している人も、今現在、機械学習を勉強中の人も、知識を確認、復習するつもりで見ていって貰えたら光栄です。）

※過学習：学習データに対してはきちんと正解できるけど、未知のデータに対しては全然当たらないモデルの状態
※汎化性能：未知のデータへモデルがどれだけ対応できるかを表す

そもそも交差検証（cross validation／クロスバリデーション）とは？

まず交差検証（cross validation／クロスバリデーション）とは、過去にコチラの記事でも紹介していますが、訓練データと評価用の検証データを分割して性能を計測することで、特定のデータに寄らない汎化性能のあるモデルを得る方法です。

つっちー

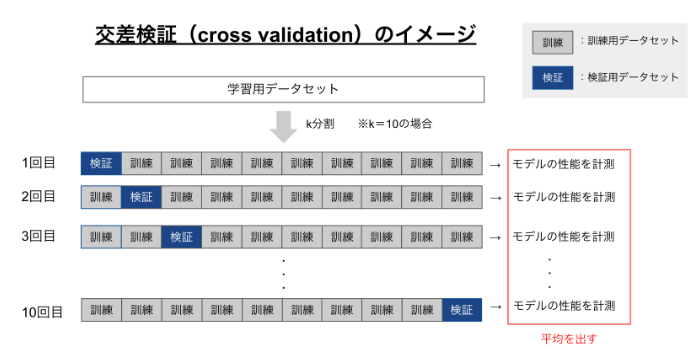
中でも一番よく使われる交差検証はK分割交差検証（k-fold cross-validation）と呼ばれる手法で、次のような流れで実行します。

図示すると次のイメージです。

なんでk分割交差検証が重要なのか？

上図からわかるように、k分割交差検証を使えば全てのデータが必ず一度は訓練セット（訓練用データセット）、検証セット（検証用データセット）として利用されるので、交差検証によって平均的に良い性能を出すモデルは全てのデータに対して良い汎化性能を示すと考えられます。

言い換えれば、モデルの性能が偶然による影響を受けないようにできるということです。例えば、「猫」と「犬」の画像認識をするために集めたデータセットを単純に分割して訓練セットを作った際、訓練セットに「犬」の画像ばかりが偶然入ったとしましょう。「犬」の画像ばかりで訓練したモデルでは、猫の画像を認識することが困難になってしまいます。

その点、k分割交差検証を使えば全ての「犬」の画像が必ず一度は訓練セットと検証セットとして利用されるので、訓練セットの抽出による偶然に影響されにくくなると言うことです。

つっちー

このように、k分割交差検証は単純にデータセットを訓練セットと検証セットに分割する方法と比べて、より安定的で徹底した手法と言えます。

k分割交差検証のデメリットは？

k分割交差検証いいじゃん！どんどんやろうよ！！と思うのはもちろんなのですが、最大の問題は計算コストが増大することです。モデルの学習とテストをK回繰り返してその性能の平均をとるので、その分計算コストが大きくなるのは避けられません。

交差検証（cross validation／クロスバリデーション）にはどんな種類があるのか？

ここまで交差検証の基本的なことについて整理してきましたが、前述したように交差検証には様々な種類があります。ここからは交差検証を種類別に見ていきましょう。コードと処理イメージについては以下のscikit-learnのCross-validationのドキュメントを参考にしています。

3.1. Cross-validation: evaluating estimator performance

Learning the parameters of a prediction function and testing it on the same data is a methodological mistake: a model that would just repeat the labels of the s…

scikit-learn

k分割交差検証（k-fold cross-validation）

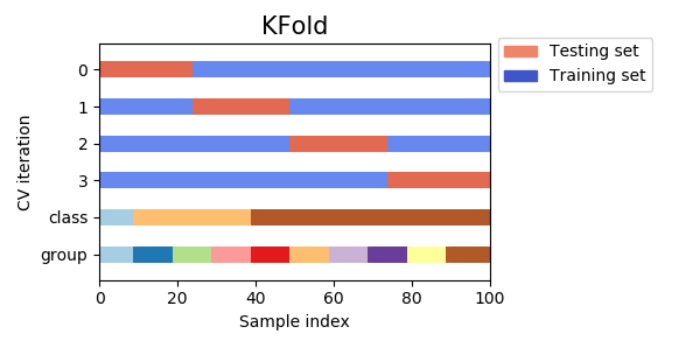
改めて、様々な種類がある中で一番よく使われる交差検証の手法がK分割交差検証（k-fold cross-validation）です。データをK個に分割し、そのうちの1つをテストデータとして使用し、残りの全てをトレーニングデータとして使用します。このようにして得られたK回の結果を平均して評価結果とする手法です。

つっちー

回帰タスクではscikit-learnは標準的なk分割交差検証をデフォルトで用います。

※以下のコードが崩れて見える方はこちらからご覧ください

＜利用例＞

import numpy as np
from sklearn.model_selection import KFold

X = ["a", "b", "c", "d"]
kf = KFold(n_splits=2)
for train, test in kf.split(X):
    print("%s %s" % (train, test))

# [2 3] [0 1]
# [0 1] [2 3]

＜処理イメージ＞

一つ抜き交差検証（leave-one-out cross-validation）

一つ抜き交差検証（leave-one-out cross-validation）は、k分割交差検証の個々の分割が、1サンプルしかないものです。つまり、K個のデータをK分割して、K回訓練とテスト（一つのサンプルをテストセットとして）を行う場合を一個抜き交差検証（leave-one-out cross-validation）と言います。

この手法はデータセットが小さい場合により良い推定が可能になります。

つっちー

ちなみにテストセットを一つではなくPつ使う場合は、leave-p-out cross-validationと呼ばれるようですね

from sklearn.model_selection import LeaveOneOut

X = [1, 2, 3, 4]
loo = LeaveOneOut()
for train, test in loo.split(X):
    print("%s %s" % (train, test))

# [1 2 3] [0]
# [0 2 3] [1]
# [0 1 3] [2]
# [0 1 2] [3]

層化k分割交差検証（stratified k-fold cross-validation）

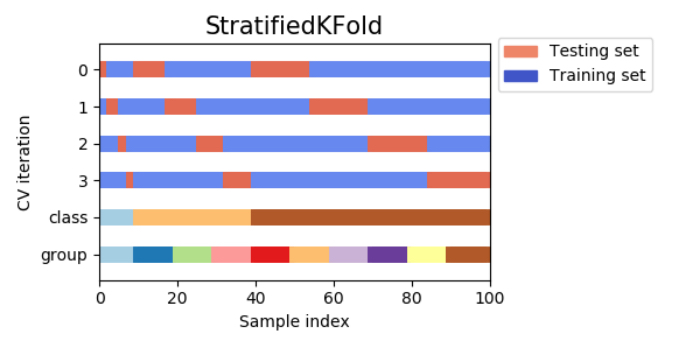
単純なK分割交差検証では、訓練セットと検証セットに含まれるクラスが全て異なる場合が起こって精度が０になってしまうことがあり得ます。例えば訓練セットが犬の画像のみだった場合、猫の画像だけで構成される検証セットに対する予測精度は0になってしまうでしょう。

こうした状況が起こることを防ぐために、クラス分類タスクでは、層化k分割交差検証（Stratified k-fold cross-validation）を用いると良いです。層化k分割交差検証では、各分割内でのクラスの比率が全体の比率と同じになるように分割します。

例えば、サンプルのうち90％がクラスAで10％がクラスBだった場合、層化k分割交差検証では個々の分割の90%がクラスAで10%がクラスBになるように分割を行うという訳なんですね。

一般的に、クラス分類器を評価するには単純なk分割交差検証ではなく層化k分割交差検証を使った方がより信頼できる汎化性能の推定ができます。例えばサンプルのうち10％しかクラスBがない場合、標準的なK分割交差検証を行うと1つの分割にクラスAしか入っていないと言うことが普通に起きてしまうため、この分割をテストセットとして使っても、クラス分類モデルの全体としての性能を評価する上ではあまり有用な情報は得られません。

＜利用例＞

from sklearn.model_selection import StratifiedKFold

X = np.ones(10)
y = [0, 0, 0, 0, 1, 1, 1, 1, 1, 1]
skf = StratifiedKFold(n_splits=3)
for train, test in skf.split(X, y):
    print("%s %s" % (train, test))

# [2 3 6 7 8 9] [0 1 4 5]
# [0 1 3 4 5 8 9] [2 6 7]
# [0 1 2 4 5 6 7] [3 8 9]

＜処理イメージ＞

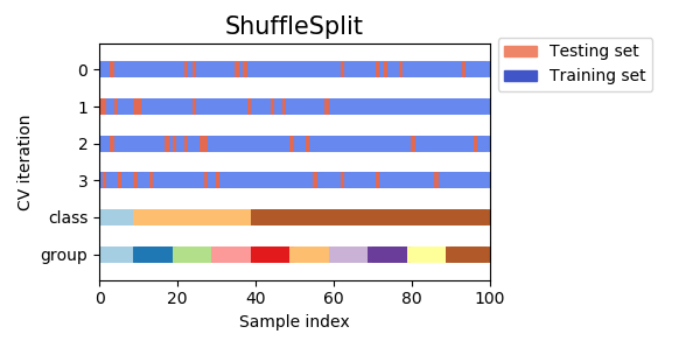
シャッフル分割交差検証（shuffle-split cross-validation）

シャッフル分割交差検証（shuffle-split cross-validation）は、毎回train_size個のサンプルを選び出して訓練セットとし、訓練セットとは重複しないtest_size個のサンプルを選んでテストセットとします。これをn_iter回繰り返す手法です！！

例えば、以下の図では10サンプルからなるデータセットを訓練セットサイズ５、テストセットサイズ２で、４回分割しています。

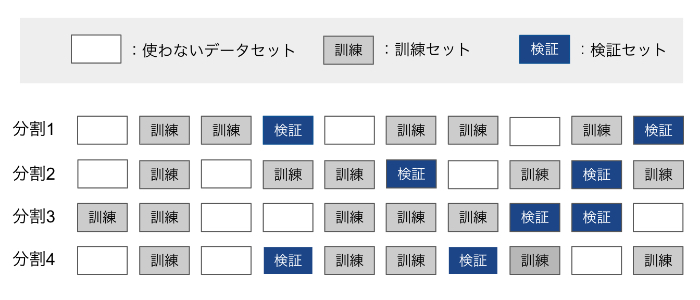
シャッフル分割交差検証では、訓練セットとテストセットのサイズに関係なく繰り返し回数を設定でき、さらにtrain_sizeとtest_sizeの和が1にならないようにすることでデータを全て使わずに一部だけを用いるように設定することが可能です。

シャッフル分割交差検証（shuffle-split cross-validation）は、データセットが非常に大きい場合に有効活用されます。

つっちー

ちなみにシャッフル分割交差検証を層化したものは、層化シャッフル分割交差検証と呼ばれ、クラス分類タスクでより信頼できる結果を得られるようです。

＜利用例＞

from sklearn.model_selection import ShuffleSplit
X = np.arange(10)
ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
for train_index, test_index in ss.split(X):
    print("%s %s" % (train_index, test_index))


# [9 1 6 7 3 0 5] [2 8 4]
# [2 9 8 0 6 7 4] [3 5 1]
# [4 5 1 0 6 9 7] [2 3 8]
# [2 7 5 8 0 3 4] [6 1 9]
# [4 1 0 6 8 9 3] [5 2 7]

＜処理イメージ＞

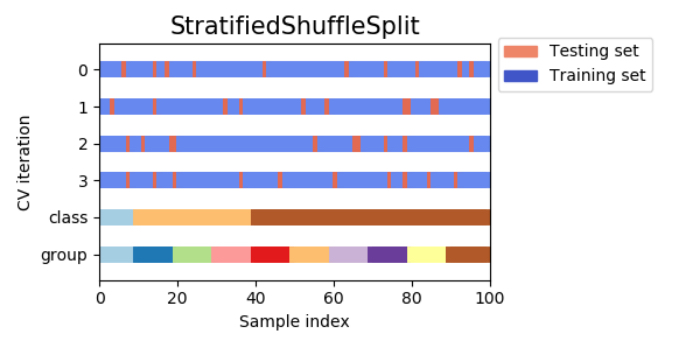
層化シャッフル分割交差検証（stratified-shuffle-split cross-validation）

前述したシャッフル分割交差検証（shuffle-split cross-validation）の特徴として、訓練セットとテストセットのサイズに関係なく繰り返し回数を設定でき、さらにデータの一部だけを用いるように設定することがありました。層化シャッフル分割交差検証（stratified-shuffle-split cross-validation）はシャッフル分割交差検証（shuffle-split cross-validation）の種類の一つであり、各分割内でのクラスの比率が全体の比率と同じになるように分割します。

＜処理イメージ＞

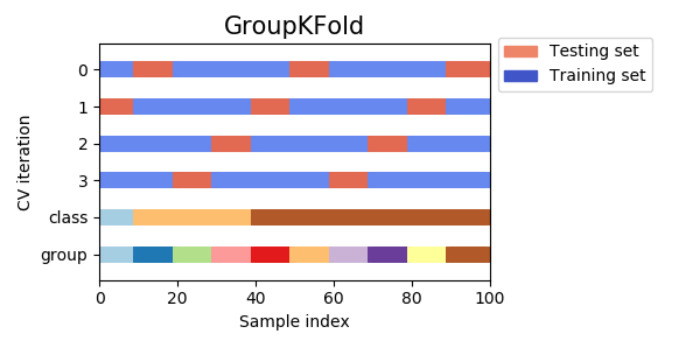
グループk分割交差検証（group k-fold cross-validation）

グループk分割交差検証（group k-fold cross-validation）は、訓練セットとテストセットで同じグループが含まれないようにするk分割交差検証です。これはどういうことかと言うと、例えば顔画像から感情を認識するシステムを作るために、100人の人が各々の様々な感情を表している顔画像を集めたとしましょう。

クラス分類モデルの目標は、データセットに属していない人の感情を正確に予測することです。このデータセットに対してもし層化分割交差検証を適用すれば、訓練セットとテストセットの両方に同じ人物の顔写真（感情は異なる）が含まれることになります。この場合、学習させたモデルが訓練セットに含まれている人物の感情を予測することは、全く見たことのない人の感情を予測するよりもずっと簡単になるのは間違いありません。

そこで、全く見たことのない人の感情を予測する精度を正確に評価するには、訓練セットとテストセットに含まれている人物が重ならないようにする必要があります。このような状況下で役立つのがグループk分割交差検証（group k-fold cross-validation）です！

グループk分割交差検証が役立つ他の利用場面として、例えば患者から得られた複数のサンプルを元に新たな患者に対する予測を行う医療用アプリや、人物の発話から得られた複数の録音データをもとに新たな話し手の発話を認識する音声認識アプリなどが該当するでしょう。

＜利用例＞

from sklearn.model_selection import GroupKFold

X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

gkf = GroupKFold(n_splits=3)
for train, test in gkf.split(X, y, groups=groups):
    print("%s %s" % (train, test))

# [0 1 2 3 4 5] [6 7 8 9]
# [0 1 2 6 7 8 9] [3 4 5]
# [3 4 5 6 7 8 9] [0 1 2]

＜処理イメージ＞

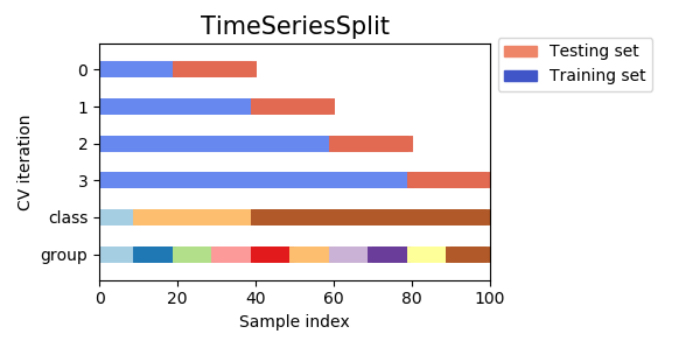
時系列分割交差検証（time series split cross-validation）

時系列分割（time series split cross-validation）は、その名の通り時系列データに使われる分割法です。

つっちー

何も考えず時系列データをk分割交差検証（k-fold cross-validation）すると大変なことになってしまうので絶対に注意が必要です！！

単純にk分割交差検証をするのでは、データの順番に意味がある時系列データををごちゃ混ぜにして、つまり未来と過去のデータを混同した訓練セットで学習を行うことになってしまい、モデルがその時点では知り得ない情報を学習してしまう事態に陥ります。これでは不当に検証セットに対する予測精度が高まる状態を避けられません。

例えば為替レートを予測するモデルを考えた場合、訓練セットに未来の値動きなどの情報が入ってしまい、予測精度は異常に高くなるが汎化性能が低いというおかしな状況が起こります。時系列分割（time series split cross-validation）を使うことでこうした問題を防ぐことが可能です。

時系列分割（time series split cross-validation）の手法としてイメージとしては、次のように訓練セットを時系列の古いデータから一つずつ付け足していきます。

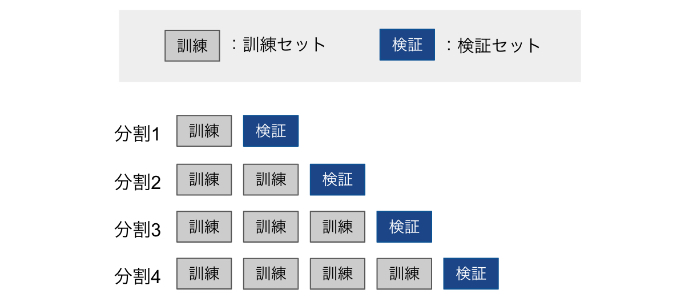
上の図を一般化すると、データが全体でnサンプルある場合に、交差検証用のデータをkサンプル確保するとすれば、

＜1回目の分割＞
訓練セット：n – kサンプル
検証セット：n – k + 1番目の1サンプルのみ
↓

＜2回目の分割＞
訓練セット：n – k + 1サンプル
検証セット：n – k + 2番目の1サンプルのみ
↓
・
・
・
というように1サンプルずつ訓練データを増やしながら学習しては交差検証をk回繰り返し、そのk回分の交差検証で得られた予測値と実測値とのRMSE（回帰の評価指標）を算出して確認するという方法です。

ただしこの方法は検証期間によって訓練セットの量が異なるため、例えば1回目と4回目の検証時のモデル精度が大きく異なる場合が普通に起こり、検証によって運用時のモデル精度を正確に把握することが難しいようです。この交差検証の手法はデータが少ない場合によく使われ、モデル運用時の精度を把握するにはデータ量と精度向上の関係も一緒に把握しておかなければなりません。

＜利用例＞

from sklearn.model_selection import TimeSeriesSplit

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])
tscv = TimeSeriesSplit(n_splits=3)
print(tscv)
TimeSeriesSplit(max_train_size=None, n_splits=3)
for train, test in tscv.split(X):
    print("%s %s" % (train, test))

# [0 1 2] [3]
# [0 1 2 3] [4]
# [0 1 2 3 4] [5]

＜処理イメージ＞

スライド型の交差検証（cross validation）

他に時系列データに対する交差検証の方法として、訓練と検証に利用するデータをスライドさせる方法で交差検証を行うやり方も効果的な方法の一つです。訓練セットのサイズをwindowで指定し、これをスライドして一定の大きさの訓練セットを常に使うやり方です。例えば、データセットを３分割し、それぞれについて訓練セットを6ヶ月分、検証セットを2ヶ月分、スライドの期間を2ヶ月分とした時のイメージは次のようになります。

つっちー

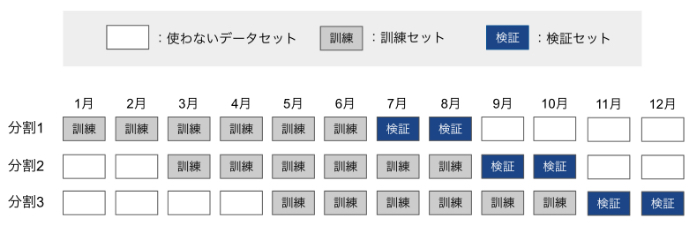
このように期間をスライドさせる形で訓練セットと検証セットを作っていくんですね！

まとめ

さて、今回は様々な交差検証（cross validation／クロスバリデーション）の種類について整理してきたので、かなり交差検証に対する理解が（僕の）深まりましたね！！

つっちー

今まで「とりあえず適当にk分割交差検証（k-fold cross-validation）使っときゃいんじゃね？」という軽い感覚でやってきた自分は、とてもヤバかったことに気づくことができました。

もう一度今回学んだポイントを整理してみると、

• 交差検証（cross validation）は単純にデータセットを訓練セットと検証セットに分割する方法よりもより安定的で汎化性能を高められる手法である
• K分割交差検証などの手法を使うことで汎化性能を高めることができる
• 分割数を増やした時の交差検証（cross validation）の最大の問題点は計算コストの増大である
• 回帰問題ではk分割交差検証がscikit-learnの標準的なデフォルトとなっている
• データセットが小さい場合にはK個のデータをK分割して、K回訓練とテスト（一つのサンプルをテストセットとして）を行う一個抜き交差検証（leave-one-out cross-validation）が効果的
• クラス分類タスクでは、各分割内でのクラスの比率が全体の比率と同じになるように分割してくれる層化K分割交差検証（Stratified k-fold cross-validation）を用いると良い
• データセットが非常に大きい場合は、繰り返し回数を設定できる＆一部のデータだけ使用できるシャッフル分割交差検証（shuffle-split cross-validation）が効果を発揮する
• 訓練セットとテストセットで同じグループが含まれていると問題になる場合は、グループk分割交差検証（group k-fold cross-validation）が力を発揮する
• 時系列データを扱う際には、未来と過去のデータが混同した訓練セットで学習する事態を避けるために、1サンプルずつ訓練データを増やしながら学習させる方法や訓練と検証に利用するデータをスライドさせる方法で交差検証を行う手法が効果的である

ということを学んできました！今回見てきたように様々な交差検証（cross validation）のやり方があった訳なんですが、他にもまだまだたくさんの交差検証があります。それらについては、今回執筆の際に参考にもさせていただいた「一流の「ものさし」職人になろう Cross Validation (交差検証)を深堀り」でわかりやすく紹介されていますので、興味のある方はぜひ参考にしてみてください。

本記事を執筆するためにTwitterで情報収集をしていたところ、「時系列データに対して単純なcross validationなんて時をかける少女か！」という内容のツイートを見つけました。今ならこのツイートの意味がわかります。

今回の交差検証（cross validation）をはじめとして、何事も理解が曖昧なまま万能ツールと錯覚して使い回すのは危険でしょう。そうならないためにも、内容や本質を理解する姿勢は日頃から大切にしていきたいものですよね！！

<参考>
・トレンド・季節調整付き時系列データの回帰モデルを交差検証してみる
・一流の「ものさし」職人になろう Cross Validation (交差検証)を深堀り
・Rでのナウなデータ分割のやり方: rsampleパッケージによる交差検証
・R言語による時系列予測とクロスバリデーション法による評価
・Time Series Nested Cross-Validation
・3.1. Cross-validation: evaluating estimator performance
・Andreas C. Muller (著), Sarah Guido (著), 中田 秀基 (翻訳) (2017). 『Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎』株式会社オライリー・ジャパン
・本橋 智光 (著), 株式会社ホクソエム (監修)(2018).『前処理大全［データ分析のためのSQL/R/Python実践テクニック］』技術評論社

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。