平均二乗誤差 MSE：Mean Square Errorが楽々わかる！回帰モデルの性能評価

AI（機械学習）を学び始めると「平均二乗誤差（MSE：Mean Square Error）」という言葉によく出会いますよね。この単語は機械学習分野に対する苦手意識をグ〜ンと高めてしまいかねない単語だと言っても過言ではなく、実際僕も最初は戸惑いました。

しかし、平均二乗誤差（MSE：Mean Square Error）は非常に重要な意味を持っているので機械学習の知見を深めたい人ならば絶対理解することが必要な単語です。そこで今回は平均二乗誤差（MSE：Mean Square Error）についてお伝えしていきます。

一言で言うと「平均二乗誤差（MSE：Mean Square Error）」とは・・・

実際の値と予測値のズレがどれだけあるかでモデルの良し悪しを判断

そもそも、平均二乗誤差（MSE：Mean Square Error）を理解するためには、線形回帰について理解しておくことが必要です。線形回帰について以下で優しく説明しているので、必要な方はこちらをご参考ください。

線形回帰

「線形回帰」という単語はAI（機械学習）を学び始めた人ならば誰しも出会う言葉ですよね。しかし、コード一行で線形回帰の処理は完了してしまうので、具体的にどういうものであるかの理解が曖昧のままの人は意外に多いかもしれません。そこで今回は線形回帰についてお伝えしていきます。

aizine.ai

線形回帰では、データの傾向やパターンを上手く表現できる線を引く（数式を求める）ことで未知のデータ（連続値）を予測するのですが、実際どのようにそうした適切な線を引いているのか（適切な数式を求めているか）気になりますよね。

※連続値・・・1.1や1.01のように繋がった値をとれるもののこと。時間や速度など

実はこの疑問に非常に関係しているのが平均二乗誤差（MSE：Mean Square Error）です。この平均二乗誤差（MSE：Mean Square Error）は何を表しているかというと、「モデルの性能がどれだけ悪いか」を示しています。

もっと具体的に言うと平均二乗誤差（MSE：Mean Square Error）は、「モデルがどれだけ悪いか」を実際の値と線形回帰モデルによる予測値のズレ（誤差）がどれだけあるかを示すものです。

なので、平均二乗誤差（MSE：Mean Square Error）の値が小さければ小さいほど良いモデルということになり、線形回帰ではこの値を判断基準として、データの傾向やパターンを適切に表現するにはどのような線を引いたら良いのか（適切なモデルを構築する）を実現しています。

具体的にどのような処理をしているかを見ていくために、直線（線形単回帰）の場合で見ていきましょう。例えば下記のようにデータがあったとします。

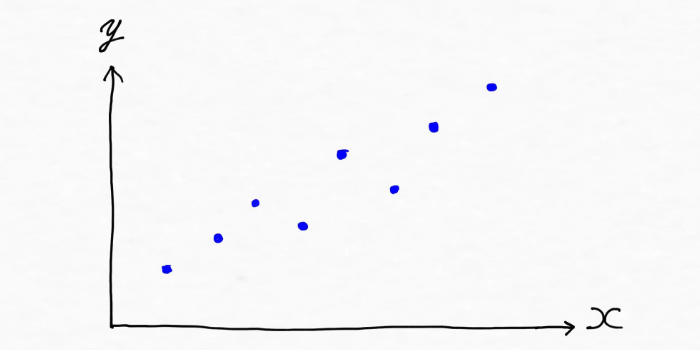
この時データの傾向やパターンを上手く表現したモデル（数式、直線）は下記のように緑の直線のイメージになりますよね。

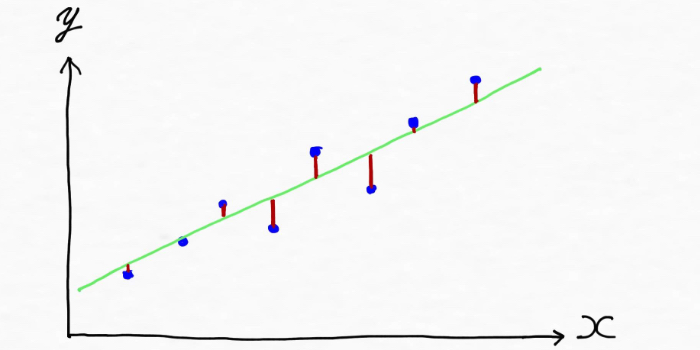
実際の値と予測値とのズレ（誤差）を赤線で示しました（実際の値から予測値に対して縦線を引いた赤の部分）。上の図はデータの傾向を上手く表現していますが、一方で例えば下記のようにでたらめな線を引いてしまえば、、、

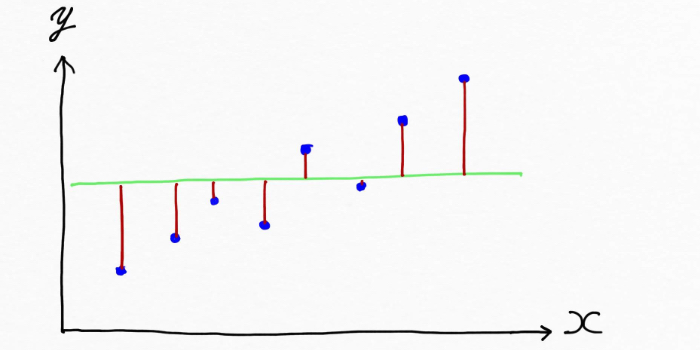
明らかにおかしいとわかります。しかも上図からわかるように赤線が長くなってしまい、ズレ（誤差）が全体的に大きくなっています。全体的な誤差が大きくなるということはもちろんその平均値も大きくなりますよね。

以上の例からわかるように、誤差が少なければ少ないほど、データの傾向やパターンを上手く示したモデルに近づきます。誤差をできるだけ少なくしたい、つまり誤差の平均値が小さくなるように線を引いていく、、、これが線形回帰モデルを構築する際に行っていることで、適切なモデルを構築するための指標が平均二乗誤差（MSE：Mean Square Error）ということです。

誤差の合計は縦の赤線の長さの合計です。ここで、誤差は（実際の値 − 予測値）で算出されるため、実際の値より予測した値が大きい場合は誤差が負の値になってしまいますよね。負の値があると正の値と足し合わせたときに誤差の大きさ（赤線の長さ）が相殺されてしまうので誤差を2乗しているというわけです。

以上を踏まえて、データが全部でn個あるとしたとき、「全部足し算するよ」の意味を持った記号であるΣ（シグマ）を用いて、実際の値とモデルによる予測値との誤差の平均値、つまり平均二乗誤差（MSE：Mean Square Error）は次のように表現できます。

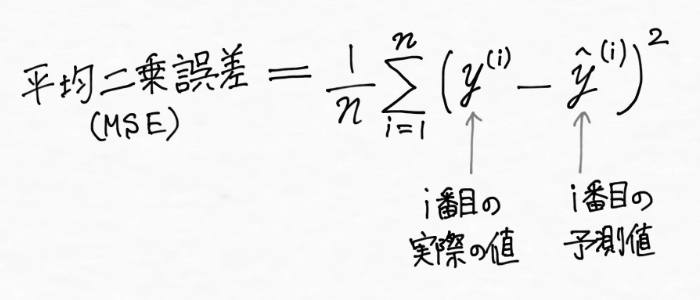
前述しましたが、モデルの性能がどれだけ悪いかを示しているこの平均二乗誤差（MSE：Mean Square Error）は値が小さければ小さいほど、データの傾向やパターンを適切に表現できているモデルだと判断することができます。

このように、どれだけモデルの性能が悪いかを示す関数は一般的に「コスト関数」と呼ばれますので、覚えておくと役立つことが多いでしょう。

平均二乗誤差（MSE）の尺度を取り直した一つの姿、決定係数（Ｒ2）

平均二乗誤差（MSE）の尺度を取り直した一つの姿に、決定係数（Ｒ²）があります。決定係数（Ｒ²）は平均二乗誤差（MSE）と同じく回帰モデルの評価指標で、決定係数（Ｒ²）＝１のとき、モデルは平均二乗誤差（MSE）＝０で完全に適合することになります。

もっと詳しく知りたい方はこちら

決定係数R2って何？は今日でお終い！3分でわかるR二乗とは

データ分析業務や統計、機械学習に携わり始めると「決定係数」や「Ｒ2」「アールツースコア」「寄与率」などの用語を見聞きして「これ何？」と頭を悩ませた経験は誰にでもありますよね。調べてみるものの、小難しい数式や説明を理解できずに憂鬱な気分になる方は多いかもしれません。そこで今回は決定係数（Ｒ2）についてお伝えしていきます。

aizine.ai

まとめ

つまり、平均二乗誤差（MSE：Mean Square Error）とは

線形回帰モデルの性能を数値化する効果的な手法の一つで、実際の値とモデルによる予測値との誤差の2乗の平均値です。下記の式で表現されます。

＜参考＞

・Andreas C. Muller and Sarah Guido　(2016).　Introduction to Machine Learning with Python: A Guide for Data Scientists.　O’Reilly Media, Inc.　（アンドレアス・C・ミューラー、サラ・グイド　中田 秀基（訳）(2017).　Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎　株式会社オライリー・ジャパン）
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗（訳）) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』

・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.

・Aurélien Géron (著), 下田 倫大 (監修), 長尾 高弘  (翻訳) (2018). 『scikit-learnとTensorFlowによる実践機械学習』

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。