一生懸命自分が努力したことへの結果が出た時には嬉しいものですよね!時間をかけて精度の高いAI(機械学習)のモデルをつくる取り組みもその一つですが、つくったモデルは性能を評価することが大事でそのためのツールに混同行列や適合率-再現率曲線、ROC曲線、AUC等があります。
これらの名称を初めて耳にした方は、
「何それ難しそう(><)」「できれば避けて通りたい(´Д` )」なんて思う方が多いかもしれません。(実際私もそうでした)
※モデル:数式で「事象を簡単にして本質(データのパターンやルール)を表したもの」
※混同行列や適合率-再現率曲線、ROC曲線、AUCの詳細は後ほどご紹介していきます
しかしモデルの性能評価は超大事で、どのくらい大事かと言えば、、、
ジャガイモの芽をちゃんと取り除くこと
ぐらい大事です。この工程を省いてしまえば手間暇かけて作ったジャガイモ使った料理も毒があるから食べれませんよね。これと同じように性能評価の工程を省いてしまえば
「精度は高いけどこのモデルは使えない」
なんてことが手間暇時間をかけて作ったモデルに対して普通に起こります。これは辛すぎる・・・(ノД`)。だからこそ、そうならないためのツールとして「混同行列」が使えると先日整理してきました。そして今回は、この混同行列に続く「適合率-再現率曲線&平均適合率」、「ROC曲線 & AUC」について理解を深めていきます!
混同行列の各指標を確認することが大事、どれを優先すべきかは扱うテーマに依存


構築したAI(機械学習)のモデルはどれだけ的中したかの「正解率」を見るだけではダメで、解決したいテーマに応じて適切な指標で性能評価をするステップは避けられません。
なぜなら、例えば100個のデータがあって90個が陽性、10個が陰性である場合、適当に「全てのデータを陽性だ!」としたら正解率は90%になりますが陰性に対する予測を全て外しているのでこれではちゃんと予測できているとは言えないからです。この例からわかるように、正解率だけを見ていてはモデルの性能評価として不十分です。
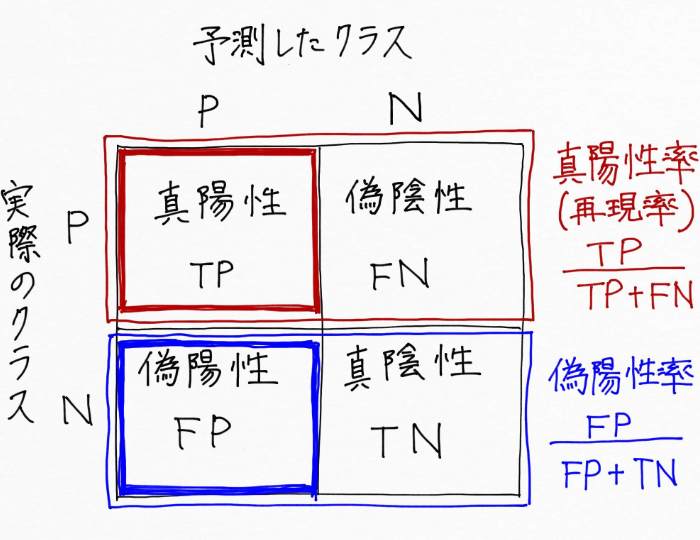
だからこそ適切な指標を見るために活用されるのが、実際のクラスと予測したクラスの関係を示した下記の混同行列です。
※下記の混同行列は、陽性:Positiveと陰性:Negativeの二つに分ける場合のもの
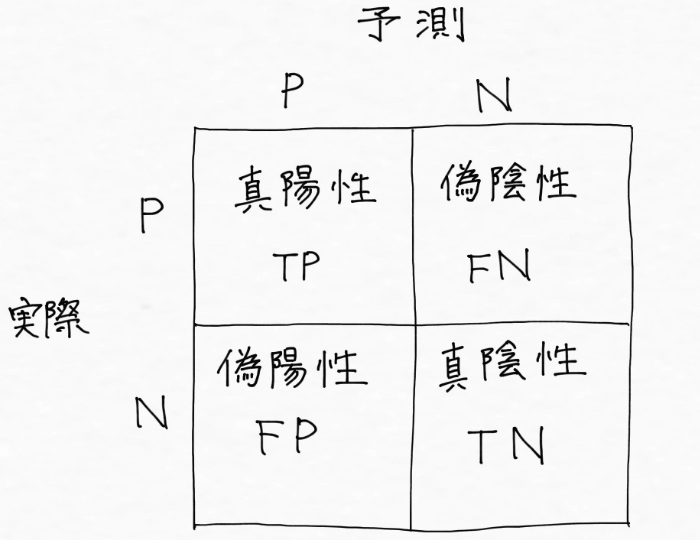

解決したいテーマに基づいてどの指標を重視すべきかを考えた上で、この混同行列から算出される「適合率」「再現率」「F値」の指標それぞれを確認することが大事でした。もっと詳しくはこちらをご覧ください。
※適合率:陽性だと予測したもののうち実際に陽性だった割合を示す指標
※再現率:実際に陽性であるものを陽性だと予測できた割合を示す指標
※F値:「適合率」と「再現率」を両方ともバランスよく表現できているかを表す指標
例えばメールがスパム(陽性)かスパムでない(陰性)かを予測(分類)したい時は、スパム(陽性)だと予測したもののうち実際にスパム(陽性)だった割合を示す指標である適合率を重視します。これは、大事なメールがスパムだと誤判定されて見落としてしまう事態を起こすよりかは多少スパムを予測できなくても良しとして考えます。
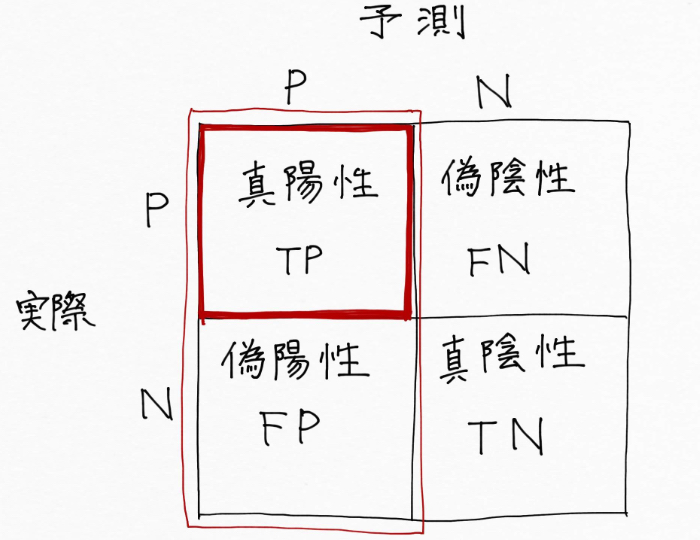

適合率は、赤枠内の赤部分(TP)の割合
<再現率を重視する場合の例>
例えば腫瘍の画像からそれが悪いものか、良いものかを予測(分類)したい時は、実際に悪いもの(陽性)を悪い(陽性)と予測できた割合を示す指標「再現率」を重視します。これは悪いもの(陽性)を悪くない(陰性)と予測して見逃しを起こすという失敗は絶対に許容できないからです。しかし、悪くないもの(陰性)を悪い(陽性)と誤って予測することが多少多くても目をつむります。再検査すればすみますので。
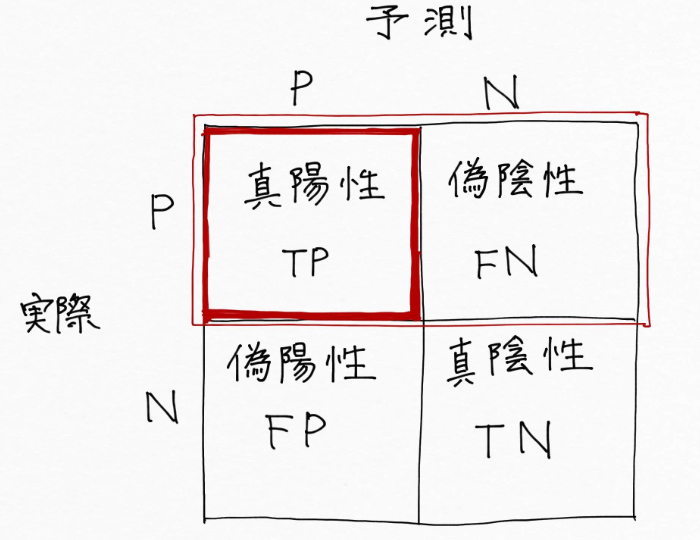

再現率は、赤枠内の赤の部分(TP)の割合
機械学習の性能評価は、正解率だけでなく、実際のクラスと予測したクラスの関係を示す混同行列から求められる各指標を確認することが大事。どの指標を優先するかは解決したいテーマを踏まえて決定する。
陽性か陰性かを判断する基準値を変更して最低限保証したい指標の値を持つモデルを構築する


混同行列から重視する指標を決めた後、
「じゃあその指標を見てモデルが活用できる品質を保証しているのかどうかという判断はどうやってするの?」
「どうやって指標の値を高めていくの?」
という疑問が出てくるんですが、この方法について調べていったところこんな文章を見つけました。
実問題を解く時には、適合率を重視するのか再現率を重視するのかを考えて、最低限保証したい方の値を決めてからチューニングするのが望ましい方法です。
<参考文献>松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.
「再現率を0.9適合率を0.5保証したい!」のようにまずはじめにゴールを設定しなさい、ということですね!クラス分類器に最低限保証したい値を設定することを「作動ポイント」の設定と呼びます。
続いて、
「チューニングするとは具体的にどういうこと?何をすればいいの?」
という疑問をさらに調べていったところ、どうやら機械学習のモデルがクラス分類(陽性か陰性かなど)を判断する基準値を変えることによって、指標の値を高めていけるということが見えてきました。
自分が「結婚願望を持つ女性」だとして、


もちろんイメージです
密かに「男性に求める10の条件」を書き記していたとします。こんな感じで・・・(職場の女性社員に書いていただきました)


この内容については色々と思うところがあるかと思いますがまあそれは置いといて、、、
この時この女性から見て
「結婚したい」と思う男性を陽性、
「結婚したくない」と思う男性を陰性
とします。
出会い系、婚活サイトへの登録、友人の紹介などを通じて色んな男性に会ったものの、中々「結婚したい」と思える男性が見つからなかったので「相手に求める私の基準に問題があるのかしら?」と思い悩んで基準の見直しを検討したとしましょう。


「年齢差は15歳以上離れててもいいかしら」「身長は180cm無くてもいいかしら」・・・・などとして基準を下げていったならば、その女性から見て「結婚したい」と思える世の中の男性(陽性)の数は増えていきます。一方で、「結婚したくない」と思う男性(陰性)の数は減っていきますよね。
基準を見直すとは次のようなイメージです。
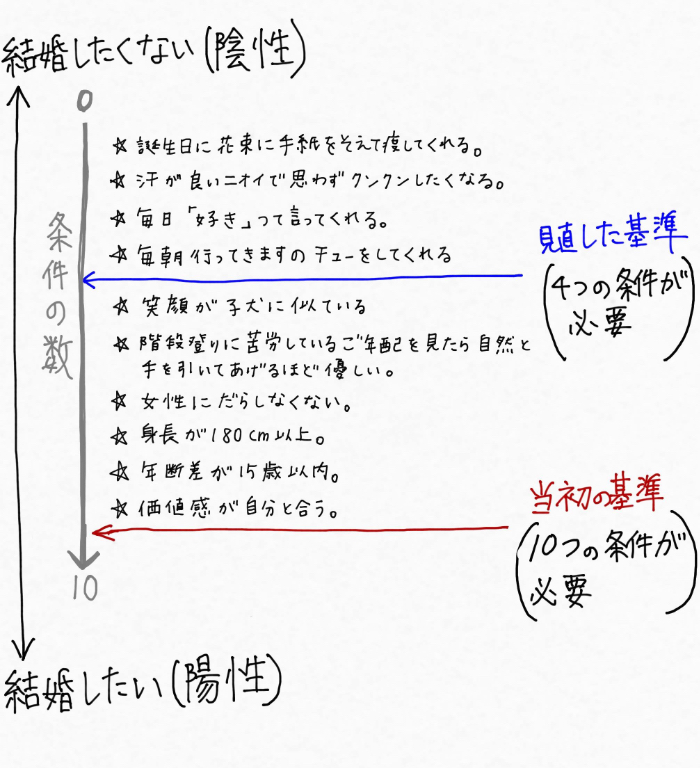

この例のように、基準を変えることによって分類される陽性と陰性の割合は変化します。つまり、これと同じようにモデルがクラス分類をする基準値を変えることで適合率や再現率を調整し、最低限保証したい値「作動ポイント」を達成できるモデルをつくっていけるというわけです。
※再現率:実際に陽性であるものを陽性だと予測できた割合を示す指標。
先ほどの例で女性から見て「結婚したい」男性の数が増えれば「結婚したくない」男性の数が減ったように、適合率と再現率は一方を追求すれば他方を犠牲にしないといけないという状態・関係(トレードオフと言われます)にあります。
AI(機械学習)の場合は、「これ陽性?陰性?」とクラス分類の判断基準となる値を「しきい値」と呼び、例えばデータから算出されたしきい値が「0.5以上ならこれは陽性、0.5未満ならこれは陰性」のようにして次々にクラスを予測していきます。
※しきい値は、英語読みで threshold(スレッショルド)と表記されたり、呼ばれる場合もある
そして、、「ちょうど良さそうなしきい値ってどうやって見つけるの?」という次なる疑問を解決してくれるのが「適合率-再現率曲線」と「ROC曲線」なんです!!
機械学習のモデルがクラス分類を行う判断の基準となる値をしきい値と言う。しきい値を変化させることによって、最低限保証したい値「作動ポイント」を達成するモデルを構築できる。適切なしきい値を見つけるのに効果的なツールとして「適合率-再現率曲線」、「ROC曲線」がある。
全ての可能な適合率と再現率の組み合わせが一目でわかる適合率-再現率曲線


モデルがクラス分類の判断をするしきい値を変えることで適合率と再現率の割合が変化しますが、取り得る全てのしきい値、つまり全ての可能な適合率と再現率の組み合わせを見られるツールが、「適合率-再現率曲線」です!
ここからはデータセットを準備して、実際にクラス分類を行いながら理解を深めていきます。
4000個のデータ(紫)と500個のデータ(黄)を準備して二つに分類していきます。
In:
#make_blobs関数を用いることで分類データセットを生成することができる
#4000点が陰性クラスで500点が陽性クラスになる、偏ったクラス分類を例に行ってみる。
%matplotlib inline
import matplotlib.pyplot as plt
from mglearn.datasets import make_blobs
X, y = make_blobs(n_samples = (4000, 500), centers=2, cluster_std=[7.0, 2], random_state=22)
plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, s=25)
Out:
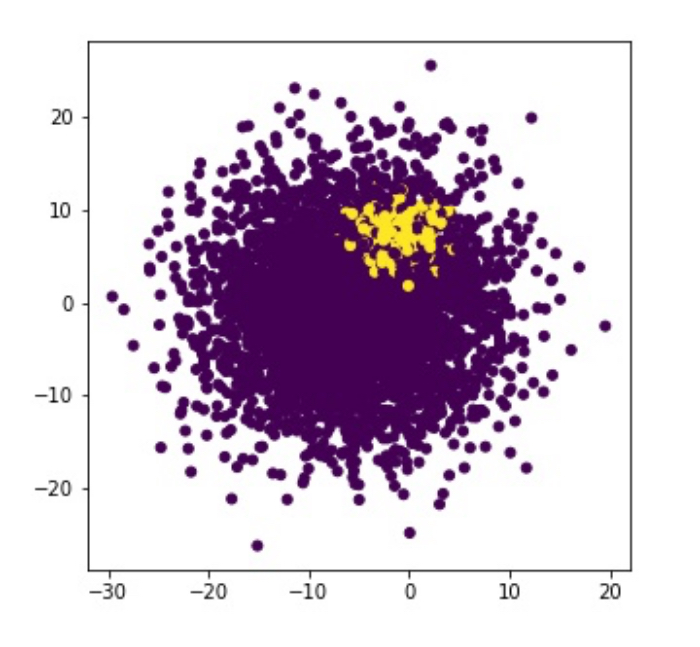

上で準備したデータを学習データとテストデータに分割後、機械学習アルゴリズム(SVC)を用いてクラス分類を行った結果について、適合率(precision )をX軸、再現率(recall)をY軸にした適合率-再現率曲線を描くと下記のようになりました。
In:
%matplotlib inline
import numpy as np
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_blobs
from sklearn.svm import SVC
#precision_recall_curve 関数をインポートする
from sklearn.metrics import precision_recall_curve
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma = 0.05).fit(X_train, y_train)
#precision_recall_curve 関数は、すべての可能なしきい値に対する適合率と再現率の値をリストをソートして返す
precision, recall, thresholds = precision_recall_curve(y_test, svc.decision_function(X_test))
#ゼロに最も近いスレッショルドを探す
close_zero = np.argmin(np.abs(thresholds))
#図のサイズを指定
plt.figure(figsize=(8, 6))
#適合率-再現率曲線を描画する
plt.plot(precision[close_zero],
recall[close_zero],
'o', markersize=10,
label="threshold zero",
fillstyle="none",
c='k',
mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.title("precision-recall curve for SVC(gamma=0.05)", fontsize=16)
plt.xlabel("Precision", fontsize=14)
plt.ylabel("Recall",fontsize=14)
plt.legend(loc="best", fontsize=14)
出ました!適合率-再現率曲線がこちら↓
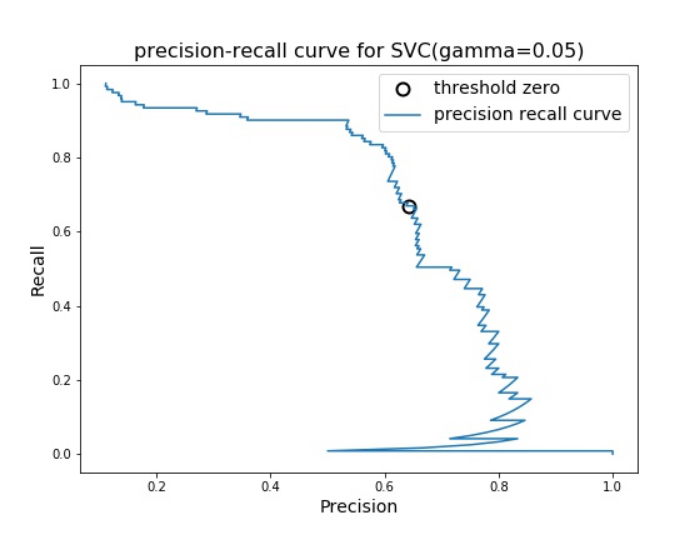

この適合率-再現率曲線を見ることによって最低限保証したい値「作動ポイント」を達成する適合率と再現率の組み合わせを確認できます。
※図中のクロマルの箇所:threshold zeroは、しきい値がモデルのデフォルトの点(しきい値=0)を示しています。
ここで改めて、適合率と再現率の意味を確認してみると、、、
適合率:陽性だと予測したもののうち実際に陽性だった割合を示す指標


再現率:実際に陽性であるものを陽性だと予測できる割合を示す指標


なので、優れたクラス分類ができる機械学習のモデルを得るには適合率も再現率も両方高い値を示すことが理想的なため、先ほどの適合率-再現率曲線の図では曲線が右上(適合率=1、再現率=1)に近づけば近づくほど良いというわけです。
適合率-再現率曲線を使えばF値だけではわからない微妙な部分を確認できる
ところで以前、適合率と再現率のバランスを表現する「F値」を確認することが性能評価には効果的だと学んできました。
けれど、適合率-再現率曲線を使えばF値だけではわからない微妙な部分を確認できます。微妙な部分を確認できるというのは、たとえば下図のようにランダムフォレストとSVMという二つの機械学習アルゴリズムを用いてそれぞれの適合率-再現率曲線を描いた時に、
In:
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=1000, random_state=0, max_features=2)
rf.fit(X_train, y_train)
#RandomForestClassifierには決定関数predict_probaはあるがdecision_functionがない
#precision_recall_curve関数の第2引数は、陽性クラスの確信度尺度なので、サンプルが陽性を意味するクラス1になる確率を渡す(陰性はクラス0)
precision_rf, recall_rf, thresholds_rf = precision_recall_curve(y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(precision, recall, label="svc")
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10, label="threshold zero svc", fillstyle="none", c="k", mew=2)
plt.plot(precision_rf, recall_rf, label="rf")
#決定関数predict_probaのしきい値は0.5、決定関数decision_functionのしきい値は0である
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(precision_rf[close_default_rf], recall_rf[close_default_rf], '^', c='k', markersize=10, label="threshold 0.5 rf", fillstyle="none", mew=2)
plt.title("precision-recall curve for svc & randomforest", fontsize=16)
plt.xlabel("Precision", fontsize=14)
plt.ylabel("Recall", fontsize=14)
plt.legend(loc="best")
Out:
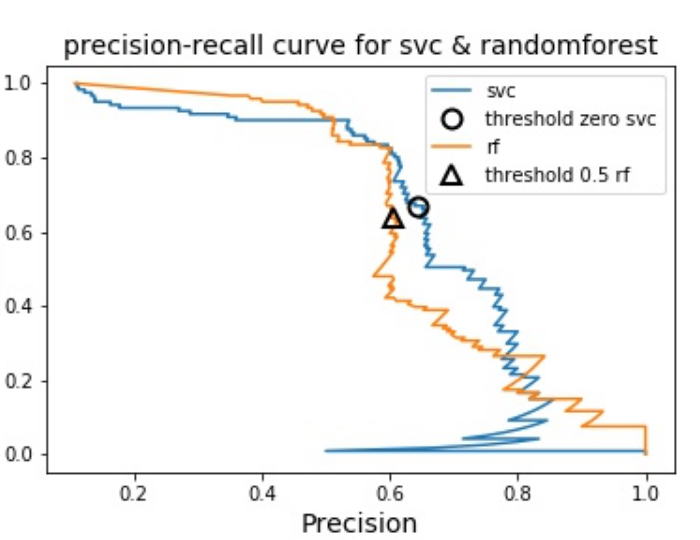

F値からはわからない以下の二点を適合率-再現率曲線から確認できるということです。
- 非常に高い再現率や適合率が必要な場合にはランダムフォレストの性能が良い
- 再現率が0.7付近ではSVMの方が性能が良い
つまり適合率-再現率曲線を用いることによって、適合率と再現率のバランスを表現する「F値」だけではわからなかった再現率と適合率のトレードオフの関係全体を確認することができ、最適な分類器の選定と性能評価が可能になります。
適合率-再現率曲線を実際に目視することで前述したような細かな情報が得られますが、自動的にモデルを比較したい!という場合には曲線の下の面積を算出して比較することが効果的です。この面積が「平均適合率」です!
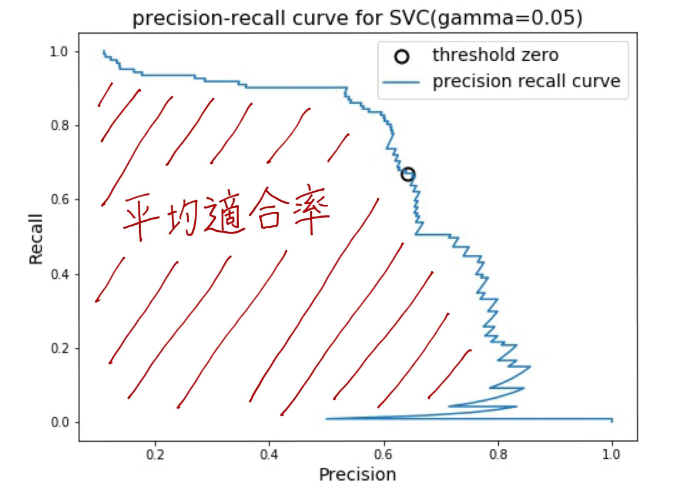

SVCとランダムフォレストによる平均適合率を算出してみると、次のようにほとんど同じ結果になりました。
In:
#平均適合率を算出する
#average_precision_score関数を用いて平均適合率を計算できる
from sklearn.metrics import average_precision_score
#平均適合率を計算するためには、まず適合率-再現率曲線を計算するつまり複数のしきい値を考慮する必要があるので、
#predictによる予測結果ではなく、決定関数であるdecision_functionまたはpredict_probaの結果を渡す必要がある
ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1])
ap_svc = average_precision_score(y_test, svc.decision_function(X_test))
print(f"Average precision of svc : {ap_svc:.3f}")
print(f"Average precision of random forest : {ap_rf:.3f}")
Out:
Average precision of svc : 0.666
Average precision of random forest : 0.662
【平均適合率】SVC:0.666、ランダムフォレスト:0.662
一方、F値を求めてみると次のように値に差が出ました。
In:
#f1値を算出する
from sklearn.metrics import f1_score
print(f"f1_score of svc : {f1_score(y_test, svc.predict(X_test)):.3f}")
print(f"f1_score of random forest : {f1_score(y_test, rf.predict(X_test)):.3f}")
Out:
f1_score of svc : 0.656
f1_score of random forest : 0.623
【F値】SVC:0.656、ランダムフォレスト:0.623
このようにF値だけをみていては、「ランダムフォレストが非常に高い再現率や適合率が必要な場合には性能が良い」ということに気づくことができません。平均適合率は、F値だけでは拾いきれない微妙な情報を与えてくれるのです。
全ての可能な適合率と再現率の組み合わせを同時に見られる「適合率-再現率曲線」を使うと、F値だけではわからない微妙なモデルの性能の判断ができる。適合率-再現率曲線を一つの値で表現する平均適合率を比較すれば、各分類器の評価が自動で可能である。
ROC曲線とは?


続いて、機械学習の性能評価に使える適合率-再現率曲線とは別のツールがROC曲線です。ROCとは(Receiver Operating Characteristics Curve)の略で、日本語にすると「受信者動作特性曲線」となって、もう・・・ナニコレ?って感じの名前ですよね(´Д` )
ROC曲線は、適合率-再現率曲線と同様にモデルの全てのしきい値を考慮した時の指標の変化をプロット(図の上に点をとること)したものです。ROC曲線の場合は、偽陽性率を真陽性率に対してプロットします。
新しい言葉が出てきたので、ここで整理しましょう。
- 真陽性率:実際「陽性」のもののうち「陽性」と正しく予測した割合(true positive rate : TPR)再現率と同じです。次の図の赤枠内の太赤部分の割合。
- 偽陽性率:実際「陰性」のもののうち「陽性」と誤って予測した割合(false positive rate : FPR)次の図の青枠内の太青部分の割合。

縦軸を真陽性率、横軸を偽陽性率としてROC曲線を描くと次のようになりました。
In:
#ROC曲線を描画する
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test))
#偽陽性率(false positive rate : FPR)
#真陽性率(true positive rate : TPR)
#x軸を偽陽性率、y軸を真陽性率としてROC曲線を描画する
plt.plot(fpr, tpr, label="ROC Curve")
plt.title("ROC Curve", fontsize=15)
plt.xlabel("false positive rate", fontsize=14)
plt.ylabel("true positive rate(recall)", fontsize=14)
#0にもっとも近いしきい値(スレッショルド)を見つける
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
出ました!こちらがROC曲線です!
Out:
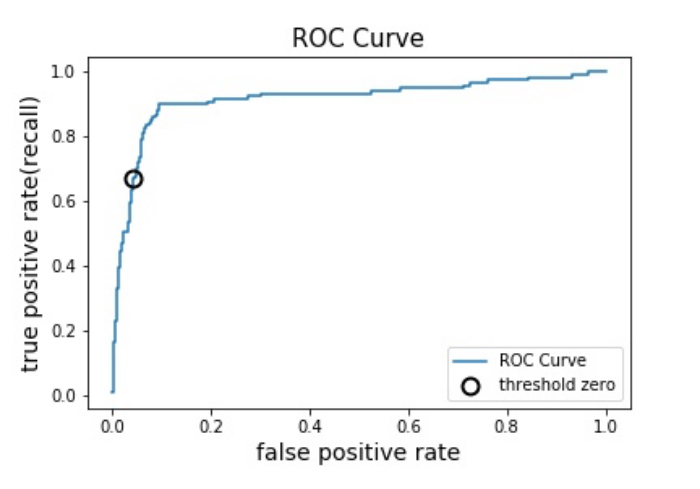

ROC曲線における理想的な点は、真陽性率が高いかつ偽陽性率が低い左上に近い点です。左上に近いほど、
実際陽性のものを正しく予測できました ( ✌︎’ω’)✌︎ ワーイ! and 実際陰性のものを誤って予測することが少なかった ( ^∀^) ホッ ということを意味します。
改めて、ROCは全てのしきい値(threshold)を考慮した時の真陽性率と偽陽性率の組み合わせをプロットしたものなので、作動ポイントを達成できるモデルを視覚的に確認、判断できますよね。
モデルがクラス分類の判断を行う全てのしきい値を考慮した時の、真陽性率と偽陽性率の組み合わせをプロットしたものが「ROC曲線」。左上に近づくほど理想的なモデルとなる。
AUCとは?
適合率-再現率曲線を一つの値で表現したい!という場合には曲線の下の面積、つまり平均適合率で表現しました。同様にROC曲線も曲線の下の領域面積を用いて一つの値で表現できます。この領域面積のことを英語でArea Under the Curve、略してAUCと呼びます。
こちらがAUCです!↓
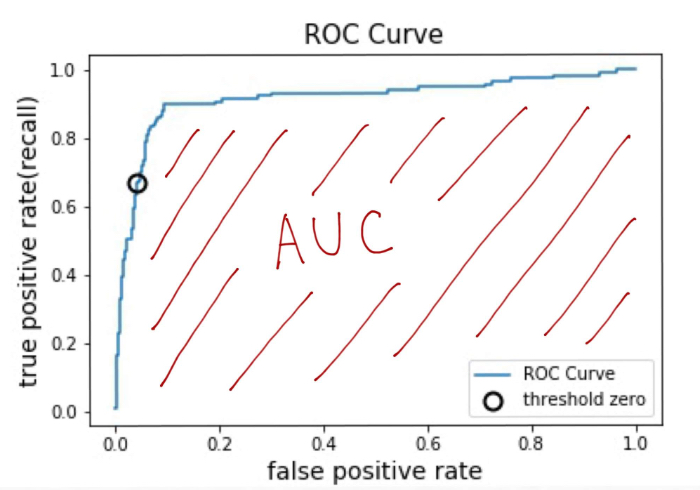

ROC曲線の縦軸(真陽性率)、横軸(偽陽性率)は0~1の範囲の値なのでAUCのスコアは常に0 〜 1の範囲になります。
完全に陽性か陰性かの予測が正確に的中している時、つまり真陽性率が1かつ偽陽性率が0になる場合は次のようにAUCは最良値の1になります。
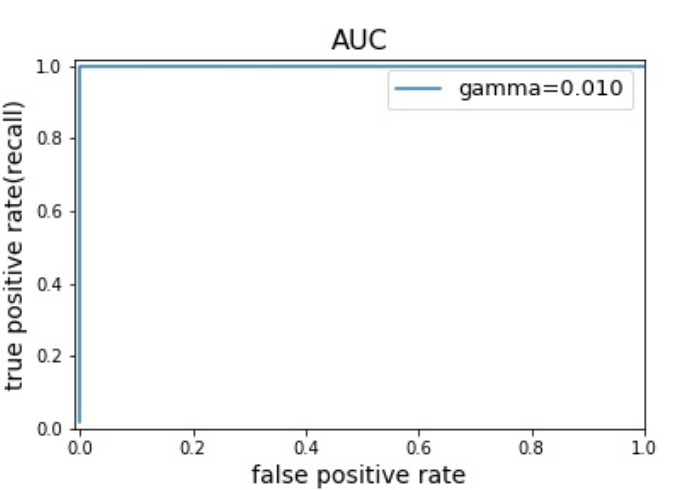

また、陽性か陰性かの判断が完全にランダムで行われている(全く予測していない)場合には、ROCが対角線となりAUCは0.5となります。
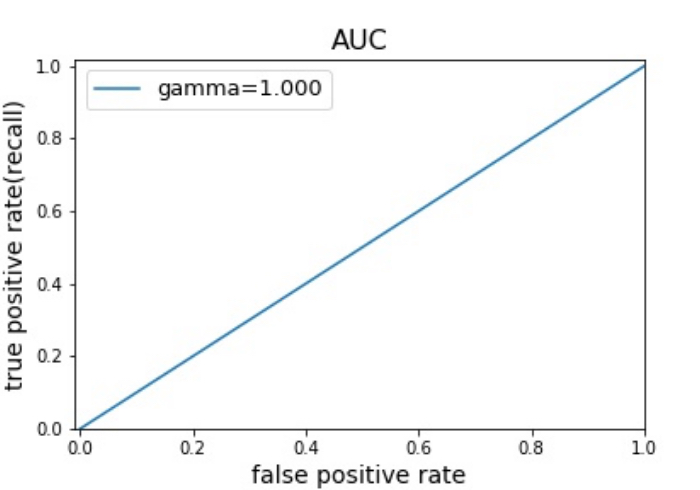

※AUCが0.5を下回る場合は、ランダムな推定よりも性能が劣るとみなされる
さて、ここで新たに別の偏ったデータセットを用意して、SVCのしきい値を変化させながら二値分類を行ってみましょう。この時の正解率(accuracy) とAUCを求めてみると、以下の結果になりました。
In;
from sklearn.datasets import load_digits
digits = load_digits()
y = digits.target ==8
X_train, X_test, y_train, y_test = train_test_split(digits.data, y, random_state=0)
plt.figure()
for gamma in [1, 0.1, 0.01]:
svc = SVC(gamma=gamma).fit(X_train, y_train)
accuracy = svc.score(X_test, y_test)
auc = roc_auc_score(y_test, svc.decision_function(X_test))
fpr, tpr, _ = roc_curve(y_test, svc.decision_function(X_test))
print(f"gamma = {gamma:.2f} accuracy = {accuracy:.2f} AUC = {auc:.2f}")
plt.plot(fpr, tpr, label=f"gamma={gamma:.3f}")
plt.xlabel("FPR", fontsize=13)
plt.ylabel("true positive rate(recall)", fontsize=13)
plt.title("AUC", fontsize=15)
plt.xlim(-0.01, 1)
plt.ylim(0, 1.02)
plt.legend(loc="best", fontsize=13)
Out:
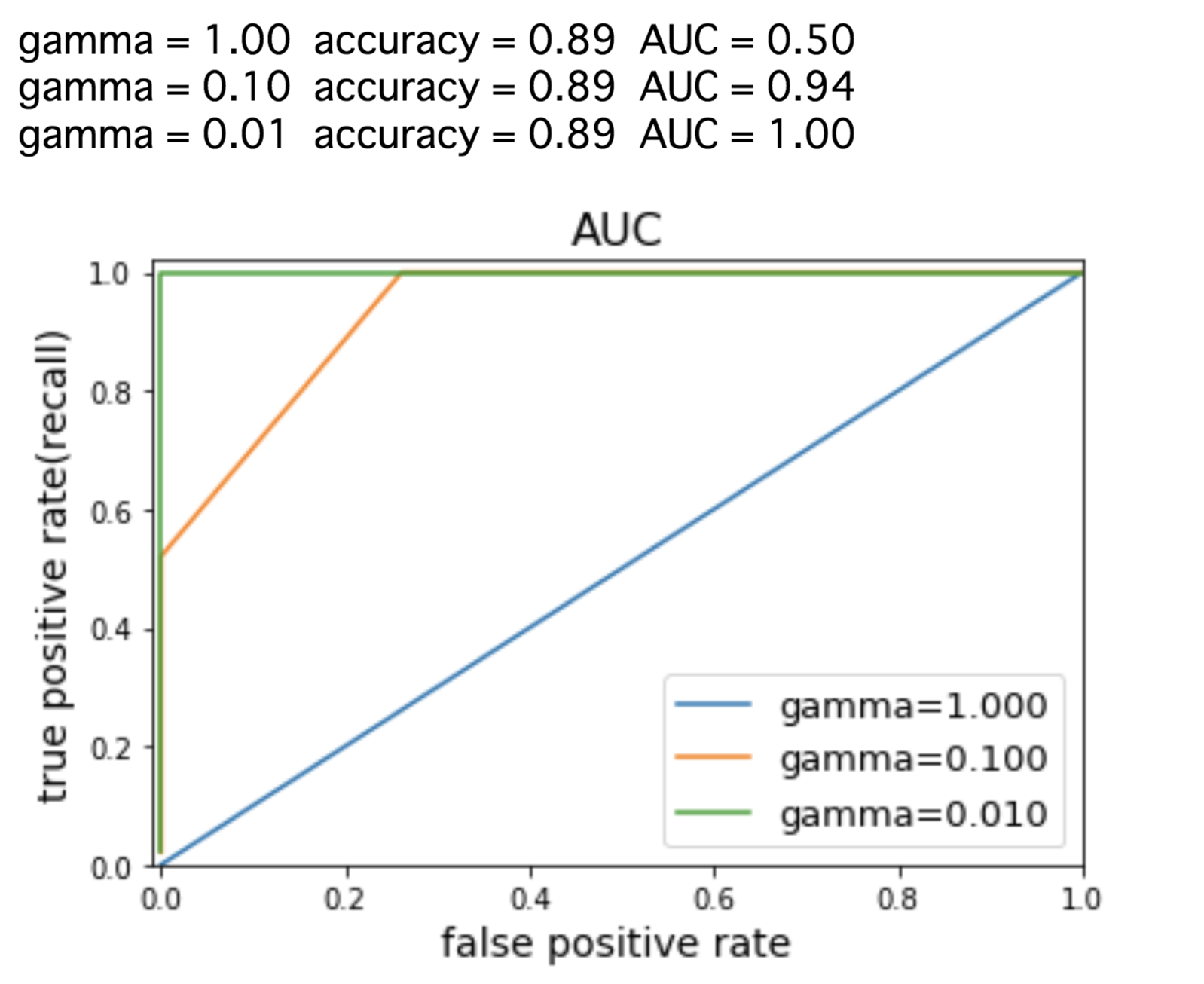

正解率(Accuracy)は常に同じ0.89ですが、AUCと対応する曲線を見ると、3つのモデルの違いが明確になっています。また、SVCのパラメータgammaを変えることでAUCの値がどんどん1に近づいていくことがわかるため、言い換えればモデルのしきい値を調整していくことで優れた予測ができるとわかります。正解率だけを見ていては決してこのようなことはわかりません。
この例のように偏ったデータを評価する際にはAUCを使用していくことが良いです。
ただAUCはモデルのデフォルトのしきい値を用いないので、AUCが高いモデルを用いて有用なクラス分類を行うには、上の例のようにしきい値を調整していくことが必要な場合があるので注意がいりそうです。
ROC曲線を一つの値で表現したい場合は、ROC曲線の下の面積の値であるAUCを使う。偏ったデータを評価する際には、ROC曲線、AUCを使用するのが良い。
適合率-再現率曲線とROC曲線、結局どちらを使ったら良いのか?


ここまで「適合率-再現率曲線」と「ROC曲線」という二つの曲線が出てきて、
「で結局どっち使ったら良いの?」
ってなりますよね。これについても調べたところ、判断の目安として陽性クラスが珍しい場合や偽陰性よりも偽陽性の方が気になるというときに適合率-再現率曲線(PR曲線)を使い、それ以外の時はROC曲線を使用すると良いようです。
例えば、前述したように大量の紫色の点(陰性)から少量の黄色の点(陽性)だけを分類する場合は、


まずROC曲線とAUCスコアを見ると、下図のように理想とする左上に近づく曲線となっているため、分類器が中々性能が高いと思いがちです。


しかし、次に適合率-再現率曲線(PR曲線)を見てみると、この分類器にはもっと右上に近づけられるということで改善の余地が十分にあることが明らかになります。
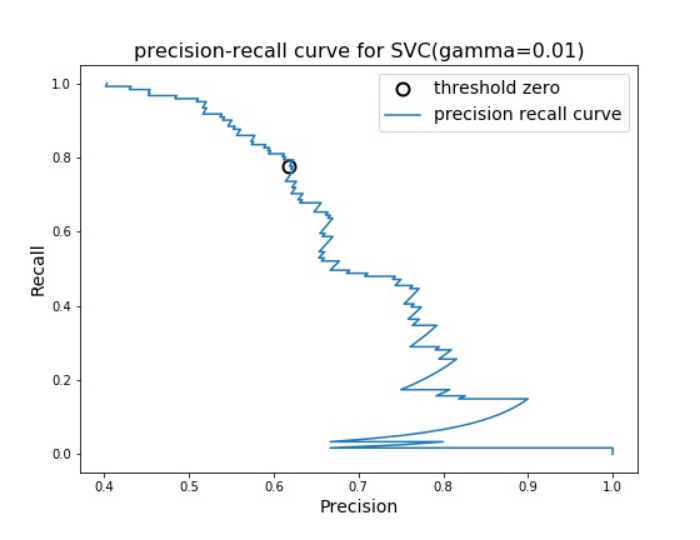

データの中身や扱う問題のテーマを踏まえて、適合率-再現率曲線とROC曲線のどちらを使用するかを選択する
まとめ
今回は、機械学習の性能評価として有効な「適合率-再現率曲線」、「平均適合率」、「ROC曲線」、「AUC」について整理してきました。ここまでを振り返って見ると、
- 機械学習のモデルを構築した後は性能評価を行うことが非常に重要である
- 目的を達成するためにクラス分類器に最低限保証したい値「作動ポイント」を設定することが重要である
- 適合率-再現率曲線は、モデルがクラス分類の判断を行うしきい値を変化させた時に適合率と再現率の組み合わせがどうなるかを示した曲線である
- 平均適合率は、適合率-再現率曲線の下の領域面積のことで、適合率-再現率曲線全体を一つの値で示す表現方法である
- ROC曲線とは、モデルがクラス分類を行うしきい値を変化させた時に真陽性率(再現率)と偽陽性率の組み合わせがどうなるかを示した曲線である
- AUCとは、ROC曲線の下の領域面積のことでROC曲線全体を一つの値で示す表現方法である
- 適合率-再現率曲線やAUC曲線を使用することで、F値だけを見ていてはわからない微妙な情報を得ることができる
- 適合率-再現率曲線とAUC曲線のどちらを使用すべきか迷った際には、陽性クラスが珍しい場合や偽陰性よりも偽陽性の方が気になる場合に適合率-再現率曲線を使い、それ以外の時はROC曲線を用いると良い
ということが整理できました。


なんとかこんな風にまとまりましたが、今回の内容は非常に専門的で何度も理解に苦しみました。
整理してみたものの、今は書籍やWebから情報を集めながら理論を理解していっているだけなのでこれからは実践が必要になります。本コンテンツを書いて情報を整理していく以外にも、機械学習のコンペティションであるKaggle等を通じて自らデータ解析に取り組む時間をどんどん作ってきたいです。
<参考>
・Andreas C. Muller and Sarah Guido (2016). Introduction to Machine Learning with Python: A Guide for Data Scientists. O’Reilly Media, Inc. (アンドレアス・C・ミューラー、サラ・グイド 中田 秀基(訳)(2017). Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎 株式会社オライリー・ジャパン)
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗(訳)) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』


AI(人工知能)って「なにそれ美味しいの?」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください(実話)。








コメントをどうぞ
説明がわかりやすいです。ありがとうございます。 専門書を買って読もうとしたのですが、10ページくらいで挫折しました。上司をなぜこの結果でよいのか説得するのに苦労しており参考になります。やはり問題は、100%正しく検出されないことで 100%が可能ならばそもそも機械学習いらないのだろうなと思い悩む毎日です。でもじゃなぜ90%でいいのか? 難しいです。
よく分からない分野ですが、噛み砕いて書いてくれてありがとうございます。夢がかないますように。
@おっさん
こちらこそ目を通してくださってありがとうございます!!