AI(人工知能)にあまり馴染みのない方にはそれほど知られていませんが、AI(機械学習)エンジニアが機械学習(※)に携わる時間の6〜8割は、機械学習モデルの実装!!・・・ではなくデータに何かしらの手を加えて綺麗に整える「データの前処理」という泥臭い作業に費やされると言われています。
ろっ、6〜8割・・・・!!
この実態に驚かれる方は多いかもしれません。なぜこれほどデータの前処理に時間が費やされるかというと、AI(機械学習)の性能はデータによって決まるからです。
もう少し詳しくいえばAI(機械学習)は過去のデータから学び、データのパターンや傾向を掴んでその内容をもとに未来の予測や判定、識別といったタスクを行います。そのため、データが悪ければAI(機械学習)の性能も悪いものになるというわけなんですね。
こうした背景もあってめちゃめちゃ大事なデータの前処理なわけですが、その中の一つに「スケール変換」と呼ばれるデータのとりうる範囲をそろえる変換処理があります。ただ、スケール変換には様々な種類があり、どういう場面でどれを使っていいのか曖昧になりがちです(僕が)。
僕は会社をクビになりながらもAI(機械学習)エンジニアを目指しているので、このような機械学習にとって重要なことを曖昧にしておくのは気持ちが悪いですし放置できません。そこで今回はデータの前処理の一つであるスケール変換に注目し、様々な手法について整理していくことにしました。
——————-補足———————-
※機械学習:AI(人工知能)を実現する技術の一つ。データからそのデータに潜むパターンや傾向を見つけ、見つけたパターンや傾向を元に未知のデータに対しても判定や予測を行っていく技術
あらためてデータの前処理がなぜ大事なのか


データが大事という話をここまでしてきましたが、機械学習アルゴリズムに準備したデータをそのまま与えても、思うような性能を得られることはほとんどありません。というのは、データというのは人がアンケートやセンサーなどを通じて集めたものなので、データが一部欠損していたり、誤って入力がなされていたり、機械の故障などで異常値が入っていたりするからです。
また、機械学習とデータの関係は僕たち人間の勉強にも似たところがあります。データの質が悪いとどうなるか?という点についてイメージしやすくなるように、例えば子供時代の勉強と機械学習にとってのデータの位置付けを比べてみると、、、
というようにデータの質が悪いと実用性の伴う機械学習モデルが構築できません。
——————-補足———————-
※機械学習モデル:機械学習アルゴリズムによってデータのパターンやルールを数式で表現したもの。このモデルによって予測や判定などの処理を行います
スケール変換をすることでなぜ多くの機械学習の性能が高まるのか


冒頭で少し触れましたが、スケール変換とはその名の通りデータのスケールを変換する、つまりデータのとりうる範囲をそろえる変換処理をすることで、これは特徴量(データにどのような特徴があるかを数値で表現したもの)のスケールを揃えるということとも言い換えられます。
そもそもこのスケール変換によってなんで機械学習の性能が高まるの?
こうした疑問を抱く人は多いのかもしれません。実際僕自身、はっきりとはわからなかったので調べてみたところ次の理由がありました。
機械学習アルゴリズムの多くは全ての特徴量が同じスケールになっていることを前提としているため、元々のデータにそのまま機械学習使うよりも特徴量のスケールを揃えた上で実行した方がはるかに上手く動作するというわけなんです。
とは言っても、特徴量のスケールを合わせる重要性はやっぱり言葉だけでは理解しづらいところがあるので具体例で考えてみましょう。
例えば、ある店舗の売上を機械学習を使って予測したいとした場合、ある1つ目の特徴量が一日の利用者数を表していて10,000、20,000、25,000、10,000、40,000という値だったとします。そして2つ目特徴量が気温を表していて7、8、7、10、5というスケールで測定されているとします。この場合、特徴量ごとに意味しているものはもちろん違うのですが、コンピュータは人間と違って区別がつきません。そのため何も指示をしないでいると、数字の大きい利用者数の方が数字の小さな気温よりもずっと大事な情報だ!と捉える可能性があります。
こうした困ったことが起こってしまうため、特徴量のスケールを変換して合わせてやることが大事なんです。
スケール変換にはどんな手法があるのか?
スケール変換には様々な手法があり、代表的なものとしては以下の4つがあります。
- 数値の特徴量が0から1の間に入るように変換する
- 平均値0、標準偏差1となるようにスケール変換する
- 中央値や分位数を用いてスケール変換する
- 個々のデータポイントの値にそれぞれ異なるスケール変換をする
以降では、これら4つのスケール変換がそれぞれどのような効果を持ち、どのような場合に活用するとよいのか、について触れていきます。
外れ値が無い時の強い味方!MinMaxScalerを用いたmin-maxスケール変換


まず一つ目のスケール変換はmin-max スケール変換(最小最大スケーリング)です。これは多くの人から正規化と呼ばれてよく使用されているので、機械学習プログラミングをしている人ならよく見聞きしているかもしれません。特徴量の値から最小値を引いて最大値と最小値の差で割る下の式で表現され、値がちょうど0から1の間に入るようにスケール変換します。
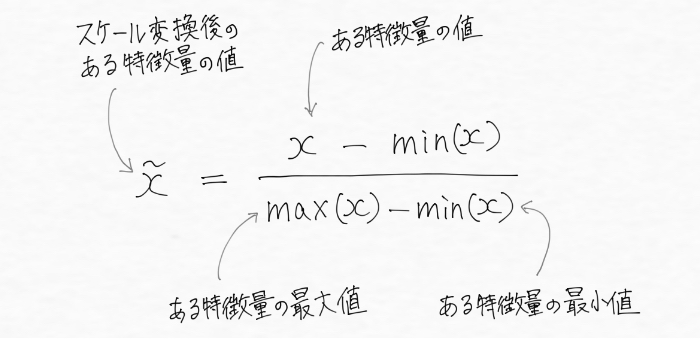

min-max スケール変換は機械学習ライブラリであるscikit-learnで実装されていて、MinMaxScalerを用いて次のように利用できます。
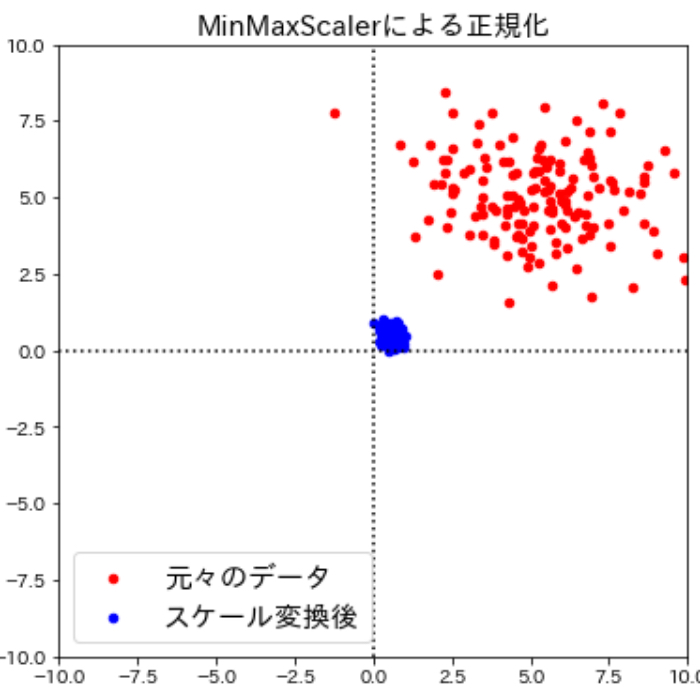

どういうことかというと、例えば変換前の値のほとんどが1〜10の値をとっていて1つだけ100,000の場合、つまり
[1、2、3、4、5、6、7、8、9、100,000]のようなデータがある場合にmin-maxスケール変換による正規化を行うと、0から1の間に入るように値が変換されるのでほとんどの値が0.0001~0.0009というめちゃくちゃ小さな範囲に押し込まれてしまい、1つだけが1というデータに変換されてしまいます。
この場合ほとんどの値が小さくなりすぎて0に近づいて意味を失ってしまっているので、min-maxスケール変換によって情報の価値が損なわれてしまっています。そのため、min-maxスケール変換を行う場合には異常に小さかったり大きかったりする値(外れ値)の有無に注意する必要があるんですね。
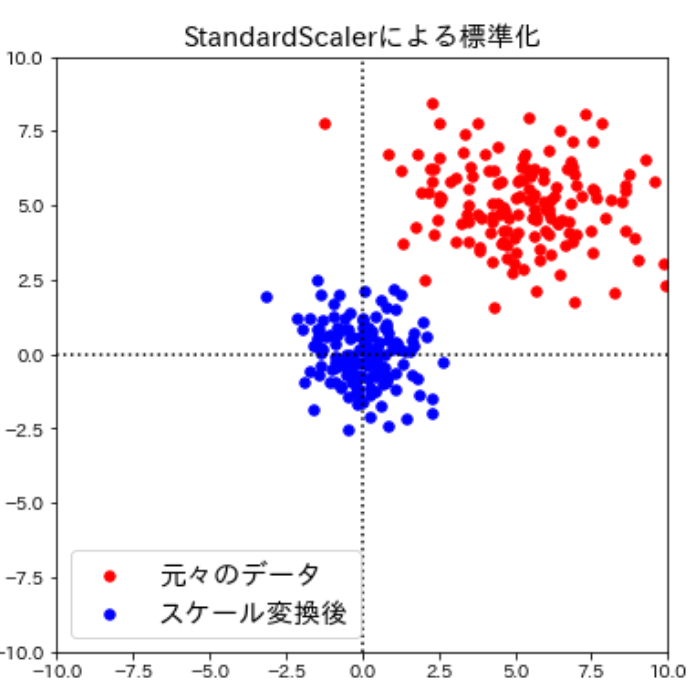
よく使われる定番といえばコレ。StandardScalerを用いた標準化(分散スケール変換)


次のスケール変換は個々の特徴量の平均が0、標準偏差が1になるように変換して特徴量を標準正規分布(※)に近似するもので、標準化と呼ばれることもあります。
scikit-learnのStandardScalerを用いて実行できるこのスケール変換は、全ての特徴量の大きさを揃えてくれますが、先ほどのmin-maxスケール変換とは違って特徴量の最大値や最小値が特定の範囲に入ることを保証するものではありません。そのため一部のアルゴリズムで問題になる場合があります。
例えば、主成分分析(PCA)(※)には平均0、標準偏差1に変換数スケール変換が適していますが、ニューラルネットワーク(※)は入力値が0〜1までの範囲に収まっていることを前提とすることが多くmin-maxスケール変換が適しているでしょう。
しかし、多くの機械学習のアルゴリズムにはこのStandardScalerを用いたスケール変換の方が実用的という見方が多いです。というのは平均値0、標準偏差1となるようにスケール変換するということは特徴量が正規分布に従うようになって機械学習アルゴリズムが重みを学習しやすくなる(※)ことを意味するからで、一般的に何か特別な理由がない限りStandardScalerを用いた方が良いようです。
——————-補足———————-
※標準正規分布:標準偏差が1で平均が0の下記のグラフ

標準正規分布
※主成分分析(PCA):主成分分析(PCA)は高次元のデータにおいてデータ全体のばらつき(分散と言います)が最大となる方向を見つけ出し、元の次元と同じかそれよりも低い次元の新しい部分空間へ射影する手法。もっと詳しく知りたい方はこちら
※ニューラルネットワーク:人間の脳内の神経細胞同士がつながってネットワークをつくっている様子を真似てコンピュータのプログラム上で再現した技術でディープラーニングのベースになっているアルゴリズム
※機械学習アルゴリズムによって構築される機械学習モデルの訓練とは、コスト関数と呼ばれる評価指標(数式)を最小化する重みの値を求めることになります。もっと詳しく知りたい方はこちら
———————————————
また、多くの場合標準化しても依然として外れ値は外れ値のままであるため、データを限られた範囲の値にスケーリングするmin-maxスケール変換とは対照的にStandardScalerを用いた標準化は外れ値から受ける影響が少なくなります。
このスケール変換は下記の式で表現されますが、
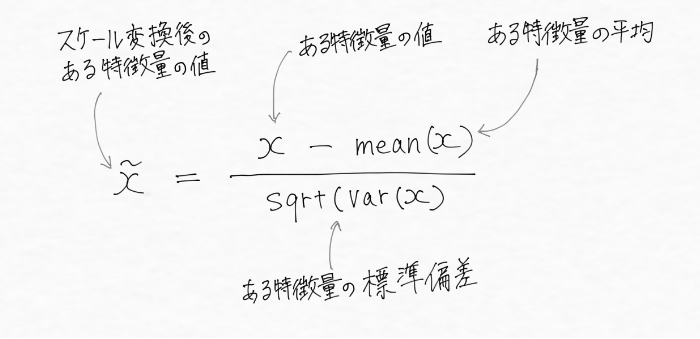

この標準化された特徴量は元の値が特徴量の平均値から標準偏差いくつぶん離れているかを示したものであることが数式からわかりますね(統計学ではZ-スコアと呼ばれます)。
標準化はscikit-learnで実装されていて、StandardScalerを用いて次のように利用できます。

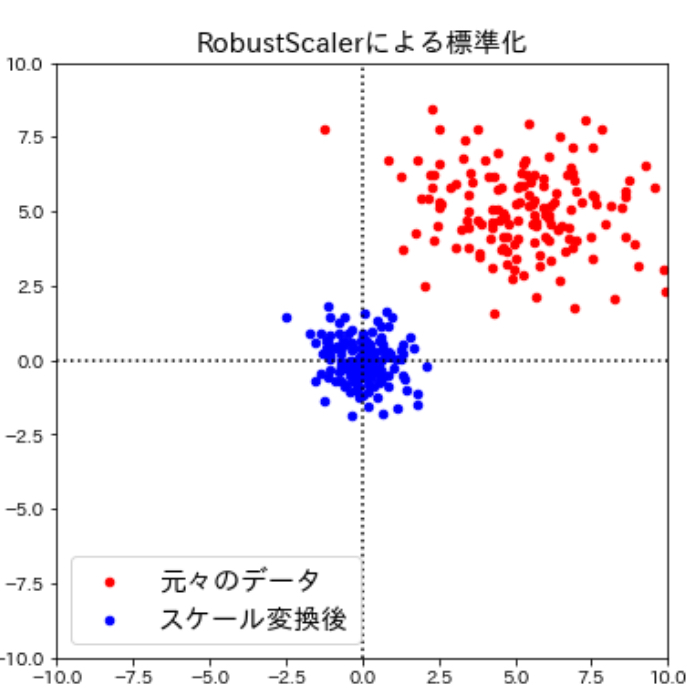
外れ値を無視するRobustScaler


続いてのRobustScalerを用いたスケール変換は、他のスケール変換方法では問題になるような測定エラーなどによる極端に他の値と異なる値(外れ値)を無視する方法です。改めてですが、外れ値があると、特徴量の平均と分散が外れ値に強く影響されるため標準化がうまく機能しません。
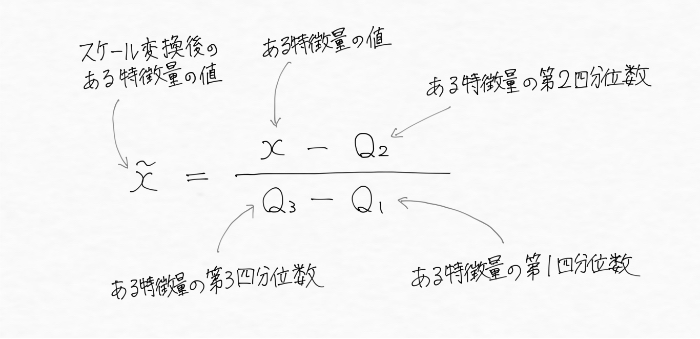
そうした場合には、中央値(※)や分位数(※)でスケール変換した方が良く、中央値や分位数を用いた標準化は以下の式で表現されます。

——————-補足———————-
※中央値:ある集合の中央値xとは、集合の半分がxよりも小さくもう半分がxよりも大きい数のこと
※分位数:第1四分位数xは全体の4分の1がxより小さく、4分の3がxより大きい数。第2四分位数xは、全体の2分の1がxより小さく全体の2分の1が大きい数(中央値)。第3四分位数xは、全体の4分の3がxより小さく、4分の1がxより大きい数
———————————————
中央値や分位数を用いたスケール変換は、scikit-learnのRobustScalerメソッドを用いて次のように実行できます。

個々のデータポイントそれぞれに異なるスケール変換をするNormalizer


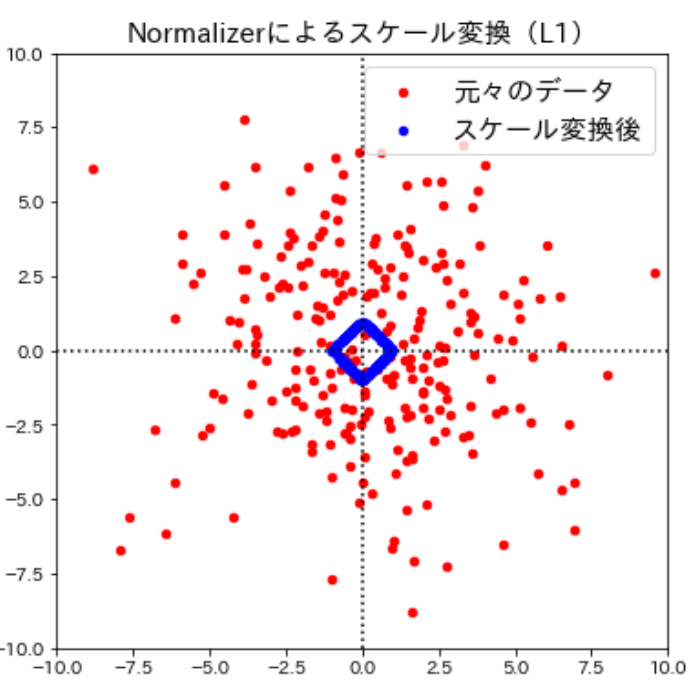
ここまで見てきたように多くのスケール変換手法はそれぞれの特徴量に対して変換を行いますが、scikit-learnのNormalizerメソッドを用いて個々のデータポイントに対してもそれぞれ異なるスケール変換を行うことができます。Normalizerは、個々のデータポイントの値をスケール変換(元のユークリッド長の逆数をかける)してユークリッド長(※)が1になるようにします。言い換えると、データポイントを半径1の円(より高次元なら超球面)に投射するということです。
言葉だけではわかりづらいので早速視覚的に確認して見ましょう。Normalizerによるスケール変換の働きをよりわかりやすく確認するためにここまでとは違うデータに対してスケール変換を実施してみます。
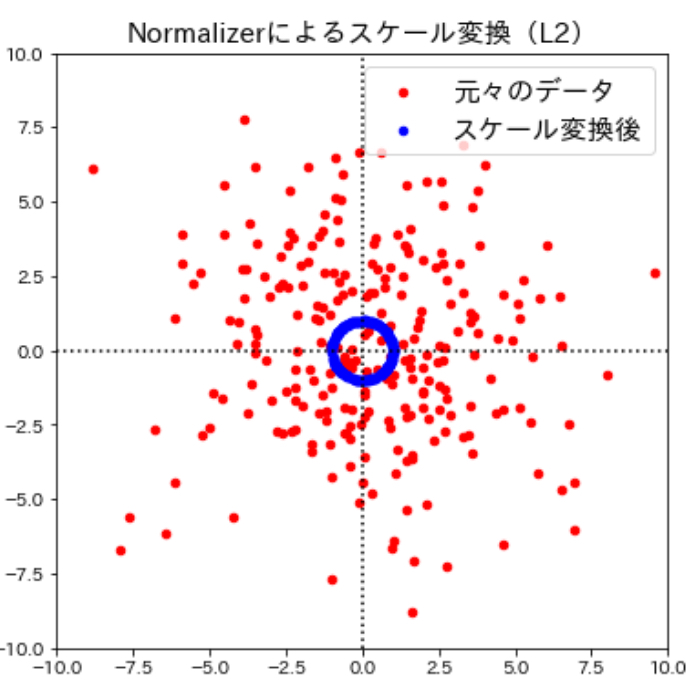

このように、Normalizerによるスケール変換は個々のデータポイントに対してそれぞれ異なるスケール変換が行われ、データの特徴が大きく変わってしまうため、この変換は方向(もしくは角度)だけが問題になる場合に用いられます。
参考までに、Normalizer()に与える対してマンハッタンノルム(L1)を指定して上記のコードを実行すると次のようになります。

決定木をベースとした機械学習モデルはスケール変換が不要
ここまでスケール変換について見てきたわけですが、決定木(※)ベースのモデルでは特徴量のスケール変換に配慮する必要がありません。なぜなら決定木ベースのモデルは数値の分割条件を値の大小関係として与えるため、特徴量をスケーリングしても閾値の値が変化するにすぎず、データポイントの分割には何ら影響を及ぼさないからです。
まとめ


さて、今回は機械学習にとって非常に重要なデータの前処理の一つであるスケール変換について整理して来ました。
本記事では複数の特徴量のスケールを揃える一般的な手法として、「正規化」と「標準化」という言葉を使ってきましたが、これらの用語は分野によってはかなり曖昧に用いられることが多く、状況に応じてその意味を推測する必要があるようです 汗
実際僕自身も今だに混乱することがありますし、ほとんどの場合正規化は特徴量を0〜1の範囲にするmin-maxスケール変換を意味しています。
振り返ってみると、
何か特別な理由がない限り、多くの場合はデータを正規分布に近づけてくれるStandardScalerを用いた標準化を行うことが良いようです。しかし外れ値に強く影響を受けてしまう場合は中央値、分位数を用いた外れ値を無視できるRobustScalerによる標準化が効果的でした。
一方外れ値がない場合はMinMaxScalerを用いた正規化によってデータが0から1の間に入るように変換することが機械学習モデルの精度を高めることに効果的でしたね!
しかし、スケール変換の手法は使用する機械学習アルゴリズムにも依存していることは忘れてはいけません。主成分分析(PCA)には標準化が適していますが、ニューラルネットワークにはminmaxスケール変換が適していました。
「機械学習はデータの前処理が命!」そんなことはすでに耳にタコができるぐらいたくさん聞いている方も読んでくださっている中にはいると思いますが、これはやっぱりとても大事なことです。いずれにせよ、今回学んだ様々なスケール変換を自分の武器として、これからの機械学習の利用に活かしていきたいですね!
<参考>








コメントをどうぞ
すごくわかりやすい記事を書いてくださってありがとうございます。
めちゃ勉強になりました!ありがとうございます!