近年アツイアツイと言われ注目されている機械学習とは、データからパターンや傾向を掴んで未知のデータを予測する、AI(人工知能)を実現するための一つの技術です。「AI(機械学習)による予測精度(※)が95%でした!!」なんて言葉を聞くと、すごーい!\(^o^)/ って思ってしまいますよね。けれど、、、
「当たり! → わーい!じゃないんです!」
これはAI(機械学習)を使ってビジネス課題を解決していくデータサイエンティストから以前僕が聞いた言葉です。この言葉を聞いた当時「ええええ!?」という驚きと僕は頭をガツン!と殴られたような錯覚に陥ったこともあってこの体験をよく思い出します。
同じように「え!?なんで!?」と思う人も多いかもしれませんし、実際僕はこの話を聞く以前は「性能評価なんてそんなにこだわる必要あるの?」ぐらいに思ってました。精度だけでの判断をなぜ控えるべきか、性能評価がどれだけ重要であるかを理解するには具体的なケースに落としてみるとわかりやすいです。
例えば「癌」か「癌じゃない」かを予測して分類するAI(機械学習)モデル(※)を作りたいとして、95%の精度が出たとします。すると5%の人は予測が外れることになりますよね。
「癌じゃないのに癌です」と間違われるか「癌なのに癌じゃない」と間違われるか
のいずれかになるはずです。前者の間違いは再検査すれば良い話なのでまだ許されますが、後者は命を落とすかもしれないので同じ間違いでも全く意味するものが違います。医療というシビアな領域では、このようにモデルの精度だけで性能を評価しようするのは全く実用的とは言えません。
これは「性能評価めっちゃ重要やん!!」っという思いを強くする例え話なんですが、
「じゃあ具体的にどうやって評価したらいいの?」
・・・。
というこの問いに僕は上手く答えられないわけです 汗
AI(機械学習)は、あくまで何かしらの目的(悪性腫瘍を見つける等)を達成するための手段です。僕が目指しているAI(機械学習)エンジニアは、この目的達成に対して最良の影響を与えるAI(機械学習)モデルを構築していく責任がありますが、モデルの適切な性能評価の手法を理解しておかなければ「頑張って作ったけどこれ全く使えないね」なんてことになりかねません。
そこで今回は「AI(機械学習)を自ら実装してビジネスで活用していきたい!」と考えている身として、AI(機械学習)モデルの性能評価について調べていくことにしました。
※精度:正確に分類されたサンプルの割合のこと
※モデル:数式で「事象を簡単にして本質(データのパターンやルール)を表したもの」。さまざまな機械学習アルゴリズム(機械学習の手法)がありますが、それぞれでモデルを作る方法が違っています。
※当記事は医療の診断精度ではなく、AI(機械学習)モデルの精度関する内容を記載しています
「癌」「癌じゃない」を見極めるケース(二値分類)で理解を深める
今回は悪性腫瘍(癌)と良性腫瘍(癌じゃない)のデータが含まれたデータセット(データの集まり)を用いて、「癌」か「癌じゃない」かを予測するAI(機械学習)モデルを作るケースで理解を深めていきます!!
以前僕が知識を整理したように、「癌」と「癌じゃない」を機械学習によって予測することは、機械学習の一つの手法である教師あり学習(分類)に当たります。
教師あり学習(分類)とは、簡単に言うと人間がAI(人工知能)に対して「これは「癌だよ」、これは「癌じゃないよ」って答えを教えてあげて、それをAI(人工知能)が学習して分類できるようになる手法のこと。もっと詳しく知りたい方はこちら
AI(機械学習)モデルの性能評価に使える混同行列
「扱うデータも定まったしよっしゃ調べるぞ!!」と意気込んでAI(機械学習)モデルの性能評価をする方法について調べていってわかったのは、性能を数値化して評価する指標や方法には様々あるということでした。
その中でも最も包括的な方法の一つとして「混同行列(confusion_matrix)」というものがあるのでここから整理していきます!!
まず、「癌」か「癌じゃない」かを予想する場合、どんなパターンに分けられるかを整理すると次の4つのパターンになりますよね。
- 「癌」を「癌」と予測した(辛いけど見つけられてよかった!)
- 「癌」を「癌じゃない」と予測した(あってはいけない。命を落としかねない)
- 「癌じゃない」を「癌」と予測した(再検査にドキドキ!!)
- 「癌じゃない」を「癌じゃない」と予測した(ほっ・・安心)
これを図にすると、次のようになります。
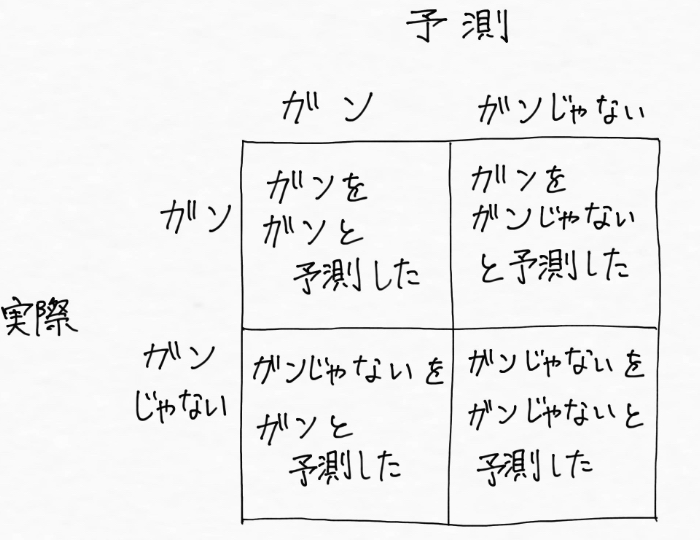

次に癌を「陽性」、癌じゃないを「陰性」、予測が当たった場合を「真」、予測が外れた場合を「偽」とすると上の図は次のようになります。
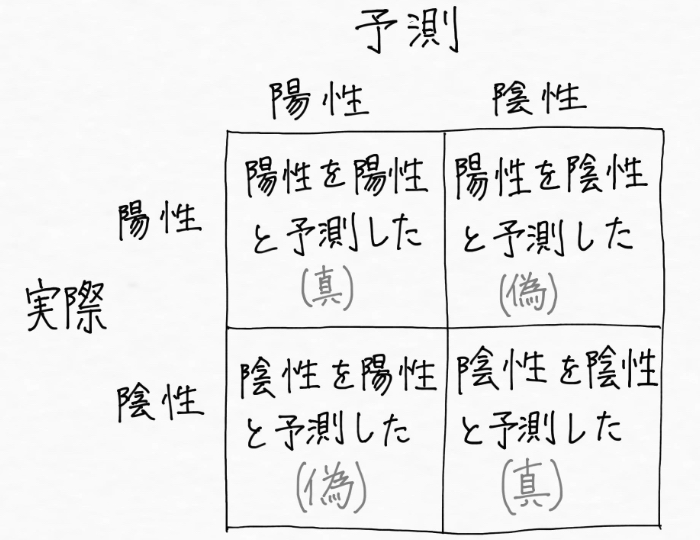

一般的に見つけたいものを「陽性 or 1」としてもう一方を「陰性 or 0」と表現するのが通例となっていて、0と1で表現できるのでこうしたケースを二値分類と呼びます。
少しややこしくなってきたかもしれません・・・ (´Д` )
さらに、陽性=Postive, 陰性=Negative、真 = True, 偽 = False として一般的に表現されるので、上の図は専門用語を用いて次のように表現でき、
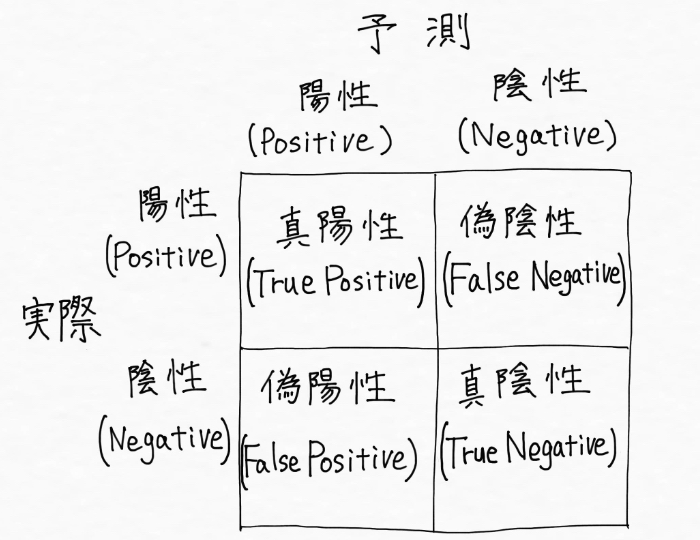

これが「混同行列(Confusion Matrix)」と呼ばれるもので、AI(機械学習)モデルの性能を明らかにするために使われる行列なんです!(「混同行列」を混合行列と混合しないようにしたいですね!実際僕はしばらくの間、間違えて覚えてました)
花びらをもぎながら「好き」「好きじゃない」「好き」・・・っていう花占いはみなさんよくやりますよね。一つの恋に一つの花占い(one love, one flower fortune )はつきものなので、積み重ねてきた甘酸っぱい花占い体験を「混同行列」で表現してみました。
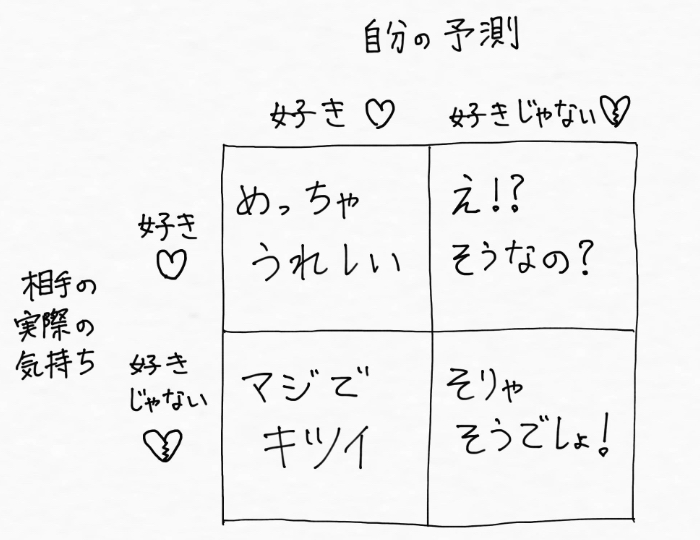

(引用 Wikipedia)
花占い(はなうらない)は、占いの一種。一般的な花占いでは、主に一見しただけでは花弁の総数がわからず、また個体によって花弁の総数に差のある花、例えばヒナギクなどが用いられる。花弁を1枚ごとにむしりつつ、幾つかの選択肢を連呼し(例えば誰かに役割を分担させるときに「Aさん、Bさん、Cさん」など、あるいは意中の人が自分を「好きか、嫌いか」などの二択)、その剰余と花弁の総数との一致で、それらの選択肢の一つを決定する。


近くの花屋さんでヒナギクを購入しました


少し脱線しましたが、先ほどの図を略称表記にして改めて見やすく整えましょう。。。
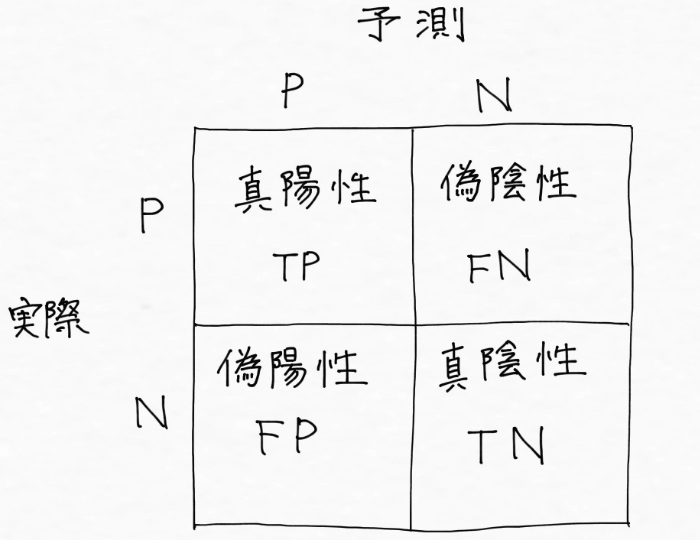

4つの領域に分類されたこの混同行列を元に、AI(機械学習)モデルの性能評価を行うことができるんです!!
僕はこの性能評価について混乱してしまって一度では理解できませんでした。ここからもう少しややこしくなっていくので、花占いで恋心を予測したらどうだったのか?のような例えも交えながら一つずつ整理していきます。
正解率(Accuracy、精度)
混同行列を見ることでわかる一つの目の指標が「正解率(Accuracy)」で、これは予測したものが実際どれだけ当たっていたかを示す割合で「精度」とも呼ばれています。赤枠内の赤の部分(TP+TN)が全体に対してどれだけの割合含まれているか、ということを表します。 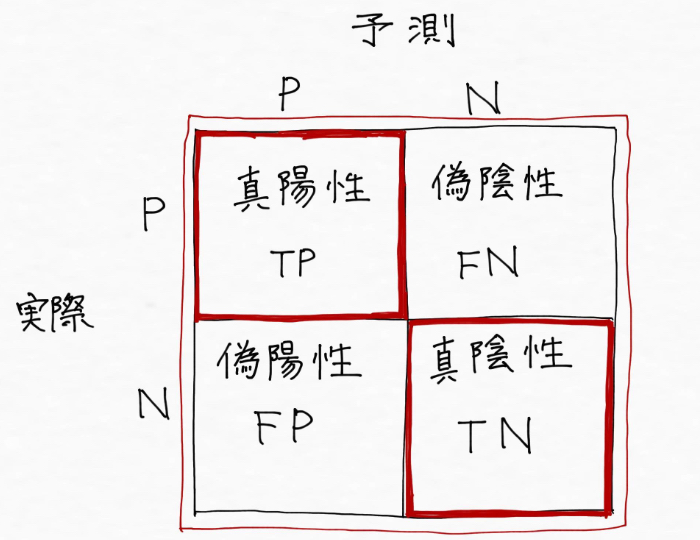

冒頭で登場した「予測精度95%ワーイ!」というのは、赤部分(TP+TN)が全体の95%を占めていたということですね〜
機械学習の分野では、分類対象のカテゴリのことをクラス(今回は「癌」と「癌じゃない」)と呼びますが、一方のクラスが他方のクラスよりもずっと多いようなデータセット(データの集まり)を偏りのあるデータセットと呼びます。
実世界では偏ったデータを扱うことが非常に多いのですが(多いらしいです)、データに偏りがある場合に正解率だけを見て決めることは非常に危険なので「ちょっと待った!!」となります。
どういうことかというと、これは例えばもしも100個のデータがあって95個が「癌じゃない」データ、5個が「癌」データだった場合、常に「癌じゃない!!」と予測したら正解率は95%になりますよね。けれどもこれでは「癌」であるものを全て見逃しているので流石におかしい。。。なのでこの例からもわかるように正解率だけを見ていてはダメでなんです。
そこで混同行列を見ることが必要になってきます!
前述した甘酸っぱい体験に例えると「正解率(Accuracy)」とは、
「あの子自分のこと好きかも」と思っていたらやっぱり好きだった。
「あの子自分のこと好きじゃないかも」と思っていたらやっぱり好きじゃなかった。
そんな「やっぱりそうだった」という割合を示すのが「正解率」のイメージです。


適合率(Precision)
偏ったデータセットの場合「正解率」だけを指標にするのは危険でした。そこで「正解率」の他に注目すべきなのがまず「適合率(Precision)」という指標で、赤枠内の赤部分(TP)の割合です。これは、癌(陽性)だと予測したもののうち本当に癌(陽性)だった割合を示しています。
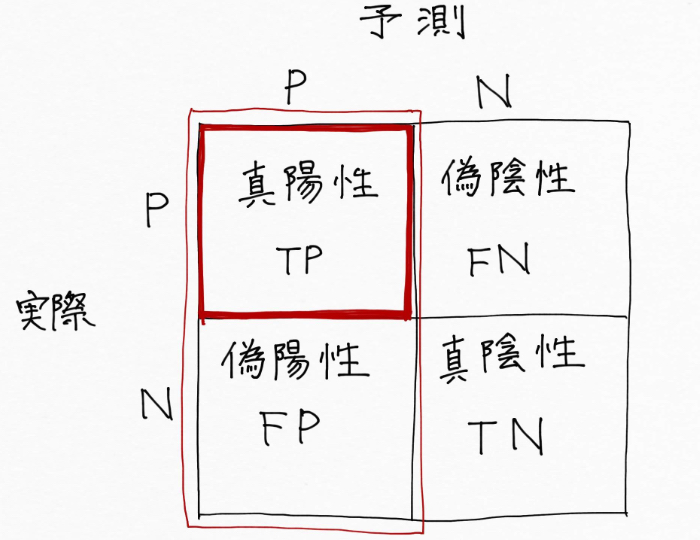

「適合率」は見逃しが多くてもより正確な予測をしたい場合に重視される指標で、これはメールが迷惑なスパムかどうかを判定する例がわかりやすいかもしれません。例えば大事なメールがスパムと誤判定されて見落としてしまった (ノД`)・・・なんて状態になるくらいだったら、たまにスパムがすり抜けてしまってもいいから、「スパムと予測したものが確実にスパムである」方が安心できます。
このように、「適合率」は見逃しが多くてもいいからより正確な予測をしたい場合に重視される指標です。
※適合率はPPV(Positive predictive value : 陽性的中率)とも呼ばれる
前述した甘酸っぱい体験に例えると「適合率(Precision)」とは、自分が恋心を抱いているけど本当の気持ちがわからない相手(何としても相手の本心を知る正確な予測をしたい相手)に対して「あの子自分のこと好きかも」という予測がどれだけ当たったかを示す指標です。
この適合率が高い人ほど、相手が自分のことを好きだとわかっていて告白できるので、思いを伝えた時の成功率が高くなる、適合率はそんなイメージでしょうか。。。
再現率(Recall)
そして機械学習モデルの性能を評価する続いての指標は再現率(Recall)で、赤枠内の赤の部分(TP)の割合、つまり実際に癌(陽性)だったものを癌(陽性)だと予測できた割合です。
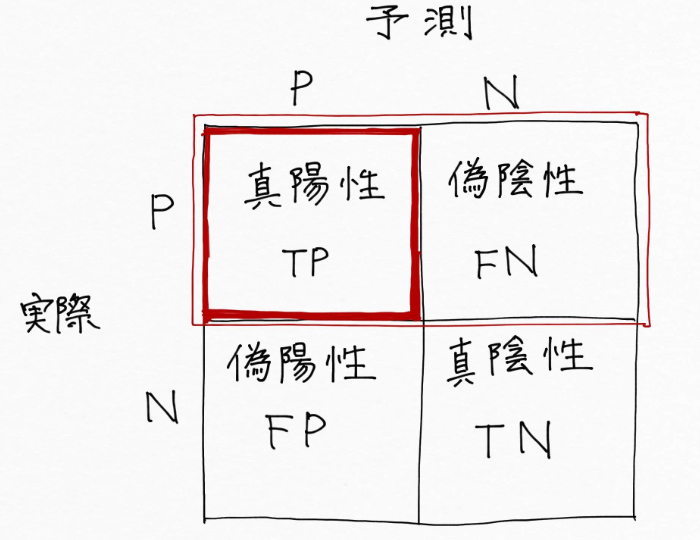

癌であるかどうかを予測する機械学習モデルを作る際には、正解率だけでなくてこの再現率を高めることが超重要!なぜなら癌(陽性)であるものを癌(陽性)であると正確に予測して絶対に見逃しをしたくないからです。予測の誤りが多少多くても抜け漏れを少なくしたい!という場合には、再現率を重視します。
前述した甘酸っぱい体験に例えると「再現率(Recall))」とは、「自分に恋心を抱いている相手を実際どれだけ把握できたか」を示す指標で、この再現率が高い人ほど他人からの好意を敏感に感じとれるので「鈍感だなあ」と言われることが少なくなりそうです。「愛するよりも愛されたい人」は高いと嬉しい指標かも・・・。
適合率と再現率はシーソーの関係


メールが「スパム」「スパムじゃない」を判定するケースでは陽性(スパム)だと予測したもののうち実際に陽性(スパム)だった割合を示す「適合率」を重視し、
「癌」「癌じゃない」を予想するケースでは実際に陽性(癌)であるものを陽性(癌)だと予測できる割合を示す「再現率」を重視しました。
癌のようなケースで「適合率」が重視されないのは、「適合率」を重視すると「これは見分けが難しいから癌じゃないことにしてしまおう・・・」という絶対にやってはいけないことが起こり得るからです。逆に「再現率」を重視して、「癌じゃない」を「癌」と予測しても再検査すれば済むので問題ありません。(再検査です!と言われた人はドキドキしますけど・・・)
このように「適合率」を重視するのか、「再現率」を重視するのかは問題によって変わってくるもので、「適合率」と「再現率」はトレードオフであることが知られています。
※トレードオフ:一方を追求すれば他方を犠牲にしないといけないという状態・関係のこと
F値(F- measure、F1スコア、F尺度)


そして4つ目の指標はF値(F- measure)です。F値とは陽性だと予測したもののうち実際に陽性だった割合を示す「適合率」と実際に陽性であるものを陽性だと予測できる割合を示す「再現率」を両方とも良くバランスよく表現できてるよね〜という指標で、図示すると次のようになります。
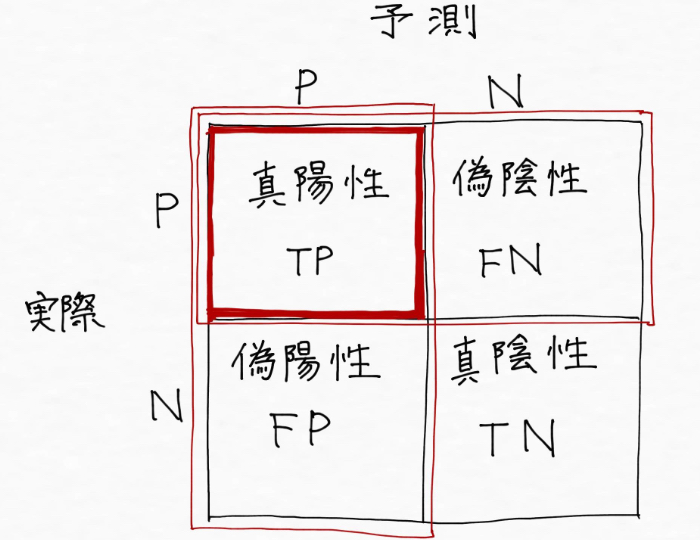

なのでF値が高ければ適合率も再現率も同じぐらいずつ当てていてバランス良く高いよね〜ということで、F値の問題点は精度と比較して解釈や説明が難しい点でしょう。
僕は最初「結局はF値を高くしたらいいんだ!!」と勘違いして理解していましたが、F値が高ければ適合率も再現率も精度が高いという訳ではなく、F値はあくまでバランスを見るための指標なんです(偽陰性と偽陽性の比率とも言えます)。
※F値は、適合率と再現率の調和平均(逆数の算術平均の逆数)です
前述した甘酸っぱい体験に例えると「F値(F-measure、F尺度)」とは、
「自分が恋心を抱いているけど本当の気持ちがわからない相手に対して『あの子自分のこと好きかも』という予測精度」と、「自分に恋心を抱いている相手を実際どれだけ把握できたかという察知力」のバランスを見るための指標です。(全部微妙な例えでごめんなさい)
このように4つの指標がありましたが、テーマによってどの指標を優先すべきかが変わって来るのでどれか一つだけを見ればいいというわけではなく、必ず正解率、適合率、再現率、F値の全てを見ることが重要なんです!
Pythonを用いて混同行列を作成してみる


悪性(癌)と良性(癌じゃない)の腫瘍データが含まれたデータセット(データの集まり)から、「癌」か「癌じゃない」かを予測するAI(機械学習)モデルの性能を実際に混同行列を用いて評価してみます!!
扱うデータセットは、Breast Cancer Wisconsin (Diagnostic) Data Setという569人の乳がんの患者データから構成されるものですが、中身を一部紹介すると次のように腫瘍の「平均半径」や「外周の長さ」など30個の測定項目(特徴量)が一人分ずつそれぞれデータとしてまとめられています(全部英語 汗)
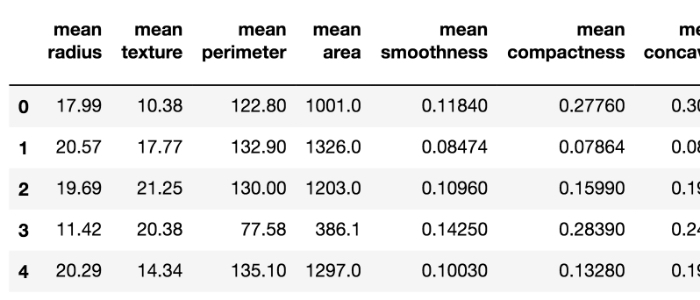

参考までに、混同行列を作るための大まかな手順は次の通りです。
- データを読み込む
- 機械学習アルゴリズムで利用できるようにデータを前処理する
- 569サンプル(行)あるデータを訓練データとテストデータに8 : 2で分割する。(訓練データ455サンプル、テストデータが114サンプル)
- 訓練データを用いて様々な機械学習アルゴリズムでモデルを学習させる
- 学習済モデルにテストデータを与えて、癌か癌じゃないかを予測させる
- 予測結果と実際はどうなのか(テストデータ)を照らし合わせて混同行列を作成する
- 正解率、適合率、再現率、F値を確認して最良の機械学習アルゴリズムを選択する
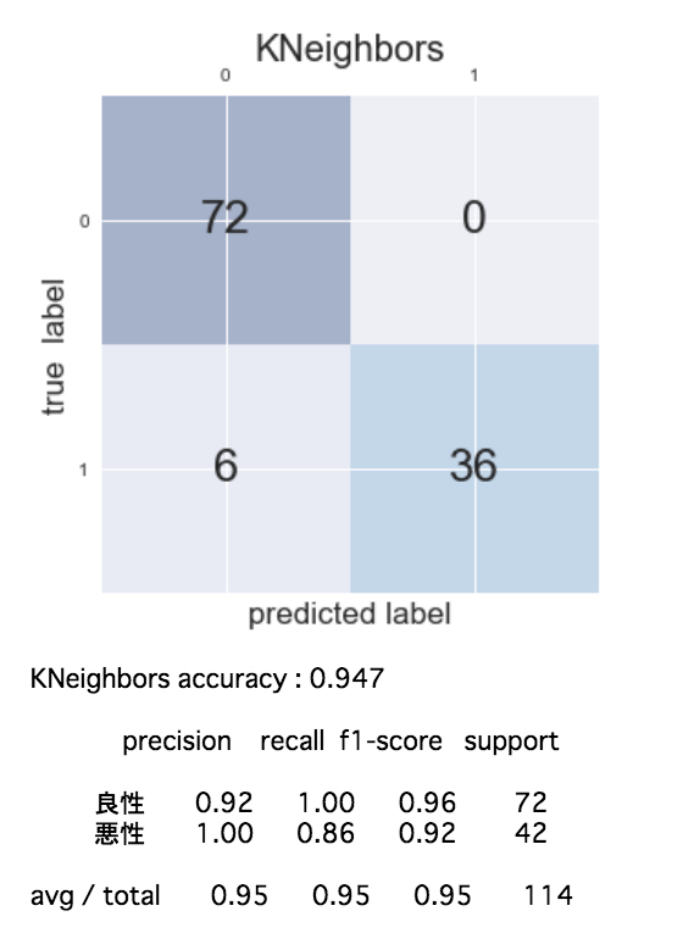
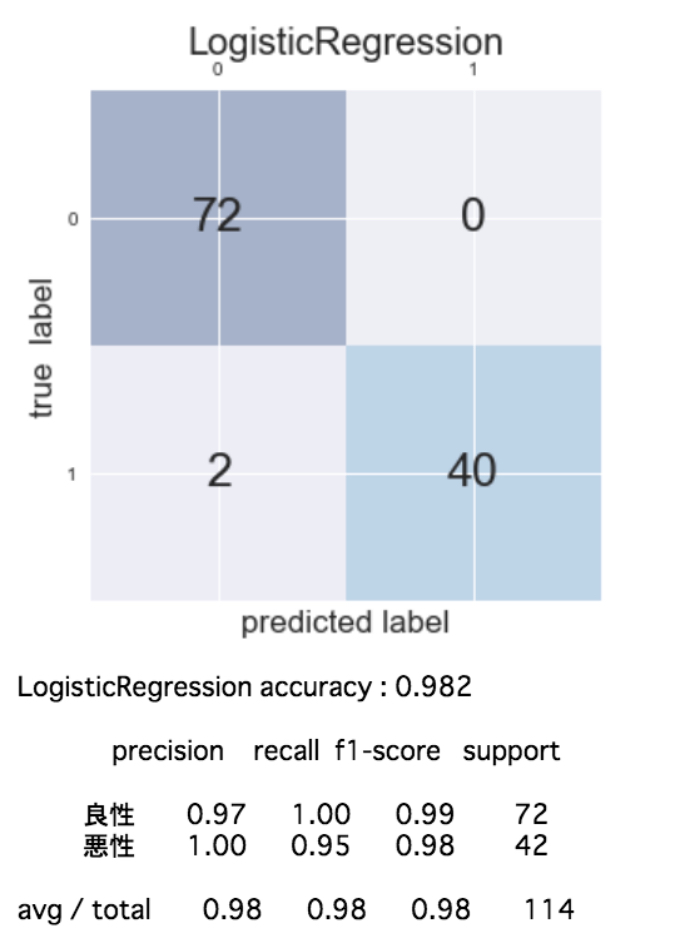
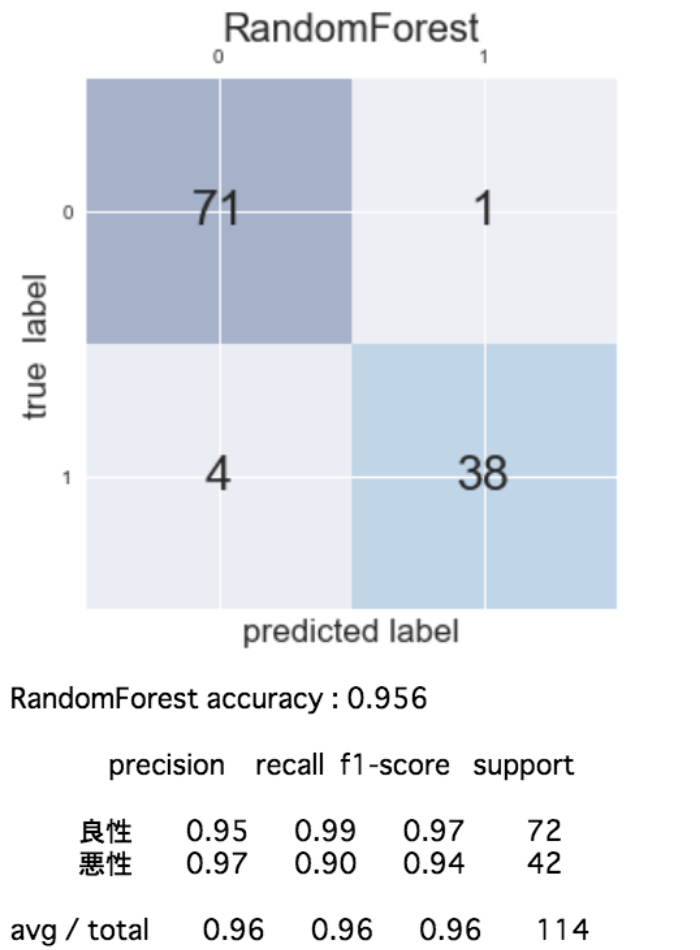
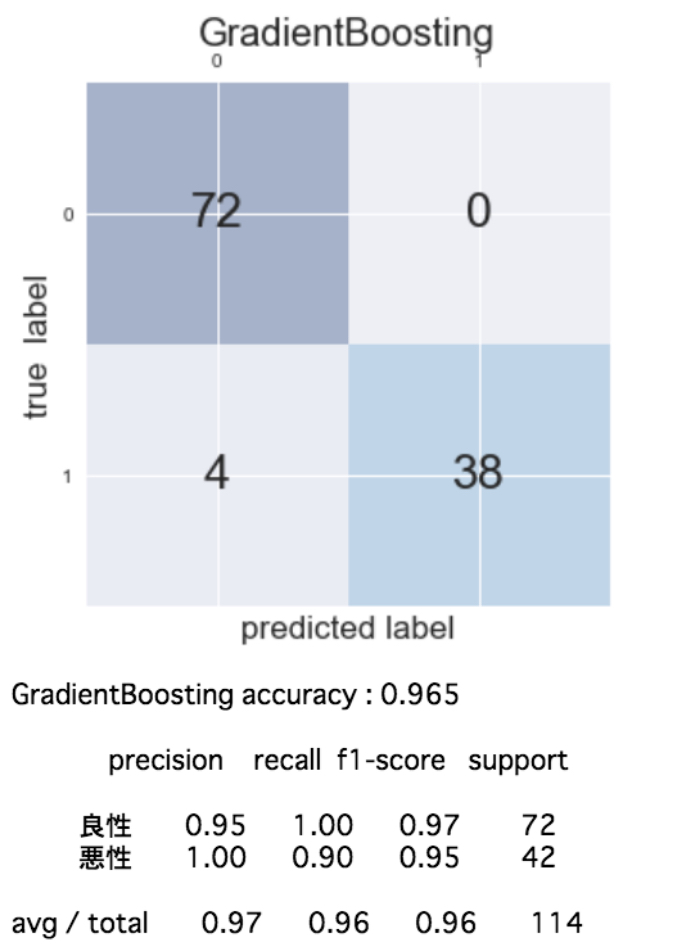
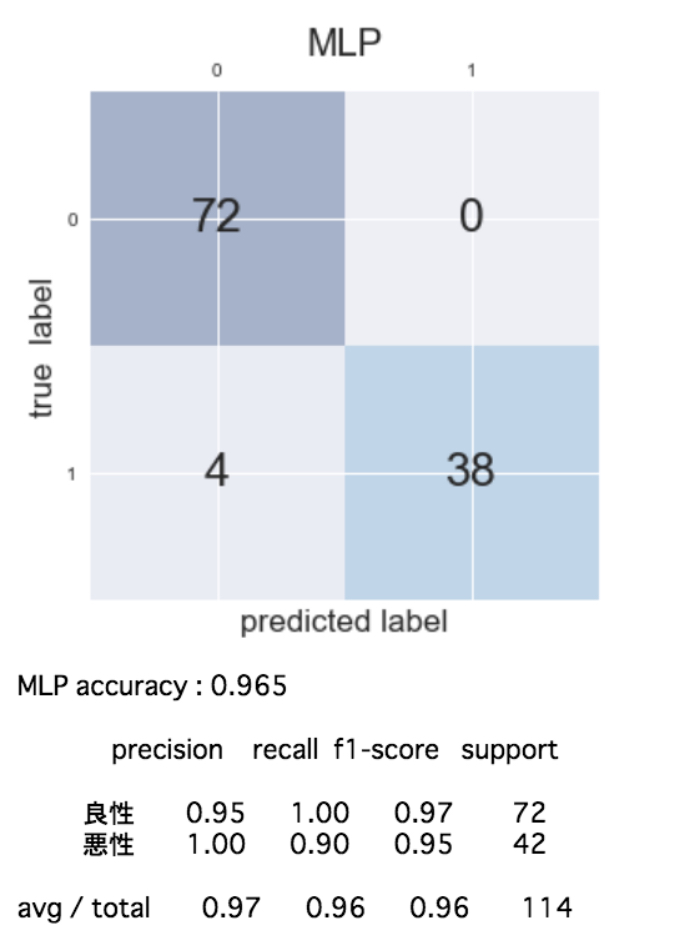
機械学習アルゴリズムを色々変えながら(6種類)混同行列を作成して各評価指標を算出すると次のようになりました。
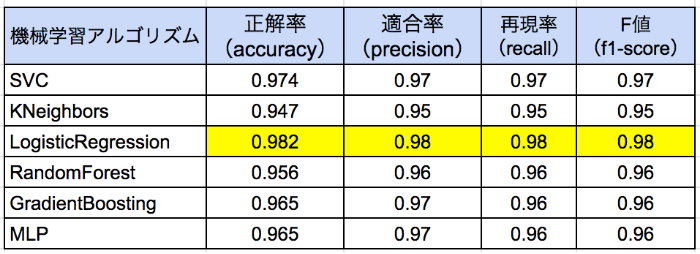

「正解率」「適合率」「再現率」「F値」の計算は面倒だなと正直思っていたのですが、一気に計算できる方法がありました!ほんと便利でありがたいです!!※興味のある方はコンテンツの最後に掲載しているコードをご確認ください。
この結果を見ると「再現率」を重視する今回のケースでは、正解率、再現率共に最良の性能を示しているLogistic(ロジスティック回帰)が適切であることがわかりました!
ただ、扱っている問題が非常にシビアで現在まだ再現率が0.98で2%の誤分類(癌を癌でないと予測)が発生するためこれでもまだ十分とは言えません。ここから先は再現率が1に限りなく近くよう、モデルがクラス分類の判断を行うための基準値(スレッショルド)を微調整するなどして試行錯誤していくことになりそう・・・。
ちなみに現実でこのような問題を解く際には、「適合率を重視するのか」「再現率を重視するのか」を考えて、最低限保証したい方の値を定めた上でハイパーパラメータチューニングをしていくのが望ましい方法だと言われています。
※ハイパーパラメータチューニング:機械学習のモデルが持っている変数を適切な値に調整すること。(もっと詳しく知りたい方はこちら)
例えば「適合率が0.9以上にならないモデルは採用しない」というように、そんな最低ラインを定めてその上でF値が高くなるようにハイパーパラメータをチューニングしてモデルを選択していくわけです。
まとめ


さて、今回は機械学習モデルの性能評価(二値分類)の方法を整理して学んできました。改めてここまでをまとめてみると、
- 機械学習モデルの性能を評価する(二値分類)には、混同行列が最も包括的で一般的な手法である
- 混同行列から「正解率」「適合率」「再現率」「F値」4つの指標を算出でき、全ての指標を踏まえた上で機械学習モデルの評価が必要である
- 正解率(Accuracy)とは、予測したものが実際どれだけ当たっていたかを示す指標
- 適合率(Precision)とは、陽性だと予測したもののうち実際に陽性だった割合を示す指標
- 再現率(Recall)とは、実際に陽性であるものを陽性だと予測できる割合を示す指標
- F値(F-measure)とは、「適合率」と「再現率」を両方ともバランスよく表現できているかを表す指標
ということを整理してきました。
一生懸命頑張ったことに対して予想以上の結果が出れば誰しも嬉しいもので例えば自分の作った機械学習モデルが高精度を出して嬉しくなるのもその一つです。けれど、頑張ったことや一生懸命やったことが「誰にとって嬉しいものになるのか」そこをちゃんと考えることがとても重要でしょう。
今回は癌の例で見てきましたが、正解率だけを見ていては患者さんやお医者さんが嬉しい気持ちになることは決してありません。機械学習はあくまで人間の暮らしを豊かにするためのツールだからこそ、誰のどんな課題を解決するためにAI(機械学習)を用いるのか?という視点はずっと大事にしていきたいです。
AI時代に大事な能力として「解決すべき問いを自ら立てる能力」がよく挙げられますが、この「誰のどんな課題を解決するために用いるのか」という視点も同じことを言っている気がします。
次回もAI(機械学習)モデルの性能評価に関する知識を整理していきます。良かったらまた覗きにきていただけたら嬉しいです!!
以降は機械学習アルゴリズムを変えて(6種類)各評価指標を算出するために用いたコードです。興味のある方のみご参考ください。
<参考>混同行列を作成&適合率、再現率、F値を出力するために今回使用したPythonコード
In:
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier,GradientBoostingClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
#乳がんの診断データの読み込み
dataset = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',header=None)
#データを目的変数と説明変数に分割する
X = dataset.loc[:, 2:].values
y = dataset.loc[:, 1].values
#カテゴリカル変数を連続値にする
le = LabelEncoder()
y = le.fit_transform(y)
#訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state=1)
#パイプラインを用いてデータのスケール変換と機械学習アルゴリズムよるモデル構築を準備する
pipe_svc = Pipeline([('scl', StandardScaler()), ('clf', SVC(random_state=1))])
pipe_knn = Pipeline([('scl', StandardScaler()), ('clf', KNeighborsClassifier(n_neighbors=10))])
pipe_logistic = Pipeline([('scl', StandardScaler()), ('clf', LogisticRegression())])
pipe_rf = Pipeline([('scl', StandardScaler()), ('clf', RandomForestClassifier(random_state=1))])
pipe_gb = Pipeline([('scl', StandardScaler()), ('clf', GradientBoostingClassifier(random_state=1))])
pipe_mlp = Pipeline([('scl', StandardScaler()), ('clf', MLPClassifier(hidden_layer_sizes=(5,2), max_iter=500, random_state=1))])
pipe_names = ['SVC', 'KNeighbors', 'LogisticRegression', 'RandomForest', 'GradientBoosting', 'MLP']
pipe_lines = [pipe_svc, pipe_knn, pipe_logistic, pipe_rf, pipe_gb, pipe_mlp]
#繰り返し処理によって、機械学習アルゴリズム別に混同行列、正解率、適合率、再現率、F値を出力する
for (i, pipe) in enumerate(pipe_lines):
#モデルを学習させる
pipe.fit(X_train, y_train)
#学習済モデルでテストデータに対して、悪性腫瘍か良性腫瘍かの予測を行う
y_pred = pipe.predict(X_test)
#実際のクラス(テストデータ)と、予測によって出力されたクラスを比べて混同行列を作成する
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
fig, ax = plt.subplots(figsize = (5, 5))
#混同行列からテストデータセットで発生した分類器の各種の誤分類に関する情報を対応づけるためにmatshow関数を使用する
#matshow関数で行列からヒートマップを描画
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for j in range(confmat.shape[0]):#クラス0の折り返し処理
for k in range(confmat.shape[1]):#クラス1の繰り返し処理
ax.text(x=k, y=j, s=confmat[j, k], va='center', ha='center', fontsize=25)#件数を表示する
#グラフを描画する
plt.title(pipe_names[i], fontsize=20)
plt.xlabel('predicted label', fontsize=17)
plt.ylabel('true label', fontsize=17)
plt.show()
#機械学習アルゴリズムごとに正解率を出力する
print(f"{pipe_names[i]} accuracy : {accuracy_score(y_test, y_pred):.3f}")
print()
#適合率、再現率、F値、サンプルの合計数を出力する
print(classification_report(y_test, y_pred, target_names=["良性", "悪性"]))
print('_'*40)
Out:
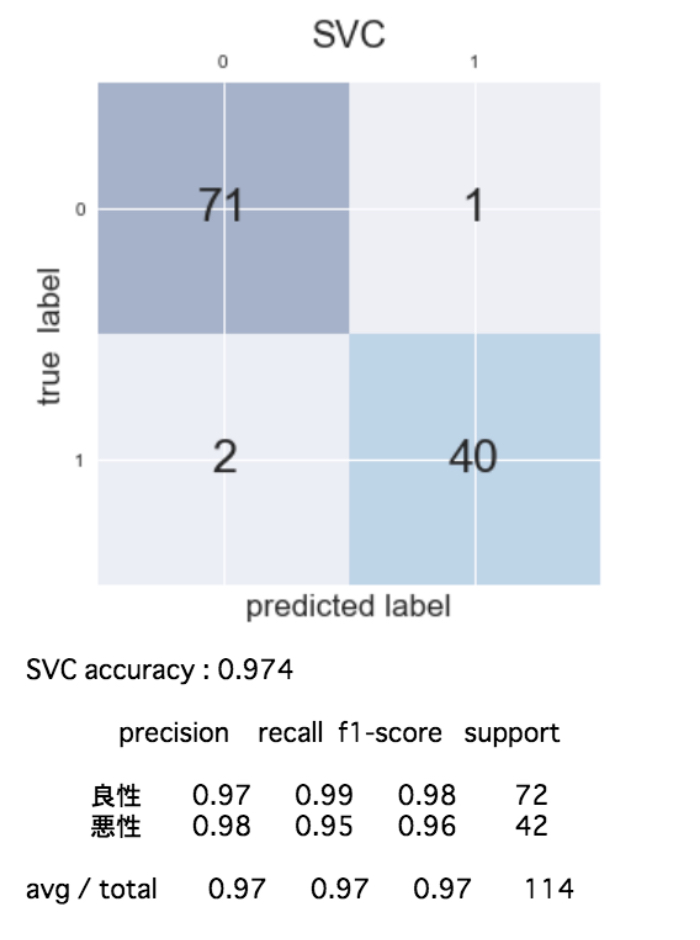






今回のように、わからないなりにAI(機械学習)の理論やプログラミングを勉強しながら日々コンテンツを作成しています。このような取り組みをすることになった経緯はコチラ↓


毎週更新していきますので、よければまた覗きにきていただけたら嬉しいです!!
<参考>
・Andreas C. Muller and Sarah Guido (2016). Introduction to Machine Learning with Python: A Guide for Data Scientists. O’Reilly Media, Inc. (アンドレアス・C・ミューラー、サラ・グイド 中田 秀基(訳)(2017). Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎 株式会社オライリー・ジャパン)
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗(訳)) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』


AI(人工知能)って「なにそれ美味しいの?」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください(実話)。








コメントをどうぞ