AI（機械学習）に対する学びを深めていると「教師なし学習」と呼ばれる手法の解説や利用するためのコードをよく見かけるので、「教師なし学習」が非常に重要であることがわかります。しかし、これが「そもそもどういうものでどんな目的でどう使うのか」について明確にしている人は少ないかもしれません。
なぜなら、現在多くの場合成功している機械学習アルゴリズムは「教師あり学習」と呼ばれるもので、機械学習の入門でよく解説されるのもこの教師あり学習だからです。
※機械学習：AI（人工知能）を実現する技術の一つ。データからそのデータに潜むパターンや傾向を見つけ、見つけたパターンや傾向を元に未知のデータに対しても判定や予測を行っていく技術
※教師あり学習：情報とその正しい判断（答え）をセットにしてコンピュータにデータのパターンを掴ませていく機械学習です
※アルゴリズム：コンピュータの計算方法、処理のやり方のことであり、色々な種類があります。
その上一般的に教師なし学習は理解するのも評価するのも難しいと言われています。しかし教師なし学習が重要な手法であり、これから機械学習を実務で活用してきたい人にとっては理解必須であることは間違いありません。
教師なし学習の代表的なものにはクラスタリングと次元削減がありますが、僕は「教師なし学習」の理解が曖昧だったため、先日「クラスタリング」についての基本を整理しました。その時の記事はこちら
けれど、もう一方の「次元削減」については理解できていない・・・です。そこで今回は、教師なし学習の理解を深めるべく次元削減とはどんなものでどういう目的でどのように使えるのか？ということを基本から順番に調べて理解していくことにしました。
そもそも教師なし学習って何？
まず、教師なし学習とは一言でいうと・・・
「正解のないデータから共通する特徴をもつグループを見つけたり、データを特徴付ける情報を抽出したりする学習手法」
です。言葉にすると理解しづらいので一つずつ見ていきましょう。
先ほど、教師なし学習の代表的なものにはクラスタリングと次元削減があると触れましたが、「正解のないデータから共通する特徴をもつグループを見つける」というのがクラスタリングに当たります。
一方で、「データを特徴付ける情報を抽出したりする学習手法」と呼ばれるのが次元削減ですが、この説明だけでは正直わかりません。一つ一つ順番に理解していきます。
教師なし学習の次元削減って何？
まず次元削減とは文字通り次元を減らすことで、高次元のデータからできるだけ情報を保存するように低次元のデータに変換することです。
（はじめ僕はこの説明では理解できませんでしたが。。。）
そもそも「次元」と聞くと、一次元はヨコの長さ、二次元はタテの長さ、三次元は奥行きの長さで・・・高次元・・？どういうこと？みたいに考えてしまいがちですが、次元を持たせる項目に特に指定はありません。
そして次元を減らす次元削減とはどういうものかというと、身近な例にするとわかりやすいです。例えば、国語、数学、理科、社会、英語という５教科それぞれの得点（これが5次元データです）を統合して、総合点という一つの指標（1次元データ）にする、、、これが次元削減の一つの例です！！
次元削減は何の役に立つのか？
次元削減がどういうものかがわかった次は、
「それは何の役に立つんだよ」
という疑問が出て来ます（僕が）。そんな疑問から調べていくと、、、出てくる出てくる次元削減の目的、そして様々なメリットたちが！！次元削減は次のように役立つことがわかりました。
高次元のデータセットを可視化してデータ同士の関係やクラスタなどのパターンがわかる
まず機械学習ではしばしば数千、数十万次元なんていう高次元のデータを扱います。数十万人の顧客履歴データから数千、数万の商品購入データを引っ張ってきて機械学習を使って分析する、というようにです。
もちろん人間はそのデータを直接グラフに表したりして見ることができません。3次元に生きている私たちですから、5次元、6次元なんていう空間ですら想像もできないわけです。
しかし次元削減を行えば、高次元のデータセット（データの集まり）を2~3次元にまで下げることができ、高次元のデータセットをグラフにプロットして可視化できるようになるんですね。（は？どうやってやんの？っていう話は後述）
そうすればよくわからない単なるデータセットだったものが、次元削減によってデータ同士の関係やクラスタ（データの集まり）などのパターンが目で見てわかるようになる！！すごい便利！というわけです。
そしてデータ同士の関係やクラスタなどのパターンがわかれば、データは非常に扱いやすくなります。というのは、例えば顧客データを「ヘビーユーザー」「ライトユーザー」「潜在ユーザー」などに分類できれば、顧客別に効果的な施策を考えていくことができるようになるからです。
このように次元削減によって高次元のデータセットを可視化できるというのは非常に大きなメリットがあるんですね！
教師あり学習のアルゴリズムの精度向上に貢献できる
次元削減が役立つ次の場面としては、次元削減をしたデータをさらに教師あり学習の教師データにして学習させることで、教師ありアルゴリズムの精度が上がることがあります。なぜなら、次元削減は機械学習では特徴量（データにどのような特徴があるかを数値で表現したもの）の項目数を減らす処理を意味するからです。
機械学習モデル(※)の予測精度を向上させるには、予測したいものに対してより強く関連する特徴量を選択し、関連しないものは削除することが必要です。この点は少しわかりづらいですが、例えば機械学習を利用して飲食店の売上を予測したい場合に、「交通事故の件数や某テレビ局の視聴率」といった役に立たなさそうな情報まで考慮してしまうと、機械学習のモデルが複雑になって予測精度は下がってしまいます。
機械学習モデルは数式で表現されるので、いらない情報、つまりいらない変数まで考慮しなければいけないとなるとおかしくなってくるというわけです。
これは過学習と呼ばれている現象で、以前整理したことがあるので興味のある方はどうぞ
モデルを構築する際に、こうしたノイズ（不要なもの）となる情報を次元削減によって取り除き、事象の主要な特徴を表すデータのみを用いることで精度が向上する場合があります。次元削減を行うことで、より本質的なデータを抽出することが可能になるというわけですね！
※特徴量：求めたいものを特徴づけるもののことです。例えば、機械学習を利用して天気データから飲食店の売上を予測したい場合、天気や気温、湿度などの売上に寄与する情報は売上げを予測するために必要な特徴量と言います
※モデル：事象を簡単にして本質（データのパターンやルール）を数式で表したもの
適切な特徴量をつくる工程は特徴量エンジニアリングとも呼ばれ、
「機械学習の実践」とは、つまるところ特徴量エンジニアリングを行うことである
と呼ばれることもあるほど重要視されています。下記の記事で紹介していますので、興味のある方はどうぞ
メモリ使用量や計算時間を削減できる
そして、次元削減によってメモリ使用量や計算時間が短縮できる場合もあります！
前述したように機械学習ではしばしば数千、数十万、数百万次元なんていう高次元のデータを扱うため、そのまま高次元のデータをコンピュータに渡せば計算時間が非常に長くなってしまうのは避けられません。
そのため計算時間が削減できるメリットは大きく、データサイズが小さくなることで学習や推論にかかる時間の短縮も期待できます。
このように教師なし学習で行える次元削減には、高次元のデータを視覚化できるようにしたり、教師あり学習のアルゴリズム精度向上に貢献したり、メモリ使用量や計算時間を削減したりと色んなメリットがあることがあるんですね。
教師なし学習は教師あり学習のように大きな自動システムの一部として利用される場合よりも、ここまで見てきたようにデータをよりよく理解するための探索ツールとして用いられる場合が多いようです。
次元削減として有名な手法、主成分分析（PCA）とは
さて、ここまで次元削減がどういうものでどんな風に役立つかを整理してきたわけですが、大きな疑問が残ります。それは、、
「次元削減の仕組みは？」「どうやって次元削減やってんの？」
という疑問です。
これを理解するために、次元削減の有名な手法である主成分分析（PCA：Principal Component Analysis）を整理していきましょう。
この記事を読まれている方の中には、過去に主成分分析（PCA）の理解に苦しまれた方もいらっしゃるかもしれません。実際僕も中々理解ができず苦戦しましたし、いろんな参考書やWebページを当たって見たのですが、わからなすぎて何度も腹が立ったくらいです
主成分分析（PCA）は、言葉にすると理解が難しくなるので図で理解していきますが、まず次のデータは2つの特徴量x1とx2を持っています。特徴量が2つですから2次元のデータですね。
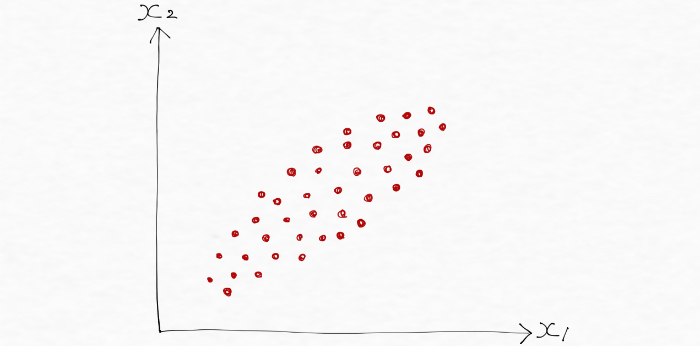
図を見ると、フランスパンのように長く細くデータが分散していることがわかります。言い換えれば、長さ方向の分散（データのばらつき）は太さ方向の分散よりもずっと大きいということですね！
さて、詳しく主成分分析（PCA）の内容について触れていく前に、ここで実際のフランスパンをイメージしてみると、上の図とは違って「高さ」があるので長さと太さと高さの3次元といえます。
フランスパンを次元削減して2次元にする方法の１つは、、、フランスパンを叩いてペチャンコにしてしまうことです！！
（高さを0にして、長さと太さという２つの情報だけでフランスパンを表現。その代わりもちろん高さの情報が失われます）
※例え話です。食べ物は絶対に粗末にしないでください
話を戻しましょう。このフランスパンのような形をした2次元のデータを主成分分析（PCA）によって次元削減する、つまり特徴量の数を減らして1次元のデータにする場合を考えてみます。
2次元のデータを1次元で表現するには、2次元空間にある全ての特徴点（データ）を1次元、つまり一つの直線上に射影する（直線上にデータを写しとる）ことで可能です。こんな風に。
※この時の直線は長さ方向です
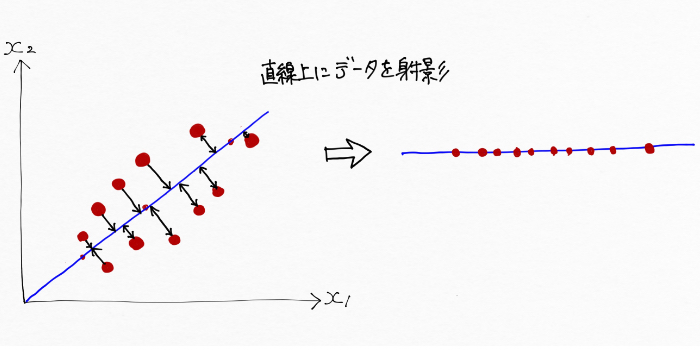
この時もちろん、実際のフランスパンをペチャンコにした時と同様に太さ方向の情報が失われてしまいますが、長さ方向の情報は保っているのでフランスパンの特徴はうまく捉えていると言えます。
このように主成分分析（PCA）は、なるべく元のデータの特徴を保ちながら（射影に伴う情報の損失を少なくして最も情報量が多くなるようにする）、フランスパンをペチャンコにしていく（次元を落としていく）方法なんですね。2次元のデータを一つの直線上に射影してしまえば、太さの情報を失う代わりにそれぞれの点が直線上のどこあるかを表現（直線だけで表現＝1次元で表現）できます。
そして今回の例の場合、主成分分析（PCA）によってデータを射影していく直線というのは、元のデータの特徴を保てる方向、つまり射影に伴う情報の損失が最も少なくなる方向で、これは分散（データのばらつき）が最大になる方向とも言い換えられます。
主成分分析（PCA）は、この分散が最大になる方向（主成分と言います）を見つけ出し、そこにデータを写しとっていくことで次元削減を図る手法です。
ここで、次の図のようにフランスパンの長さ方向を第1主成分、太さ方向を第2主成分というように呼ぶことにしましょう。
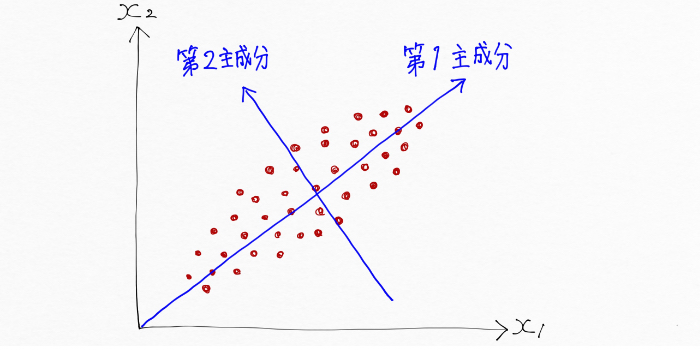
第1主成分は、フランスパンの長さ方向のデータの特徴を捉えている一方、太さ方向の特徴は捉えていません。先ほどの図のように主成分分析（PCA）によって第1主成分にデータを写し取る（射影）した時点で、太さ方向の第2主成分の情報は失われてしまうんですね。しかし、太さ方向の情報を持つ第2主成分を使えば、フランスパンの長さも太さの情報もよく捉えたものになります。
つまり言い換えれば、第1主成分と第2主成分という二つの主成分だけを用いて、フランスパンの形をした2次元のデータを表現できたと言えます。すごい！！
第1主成分に続く第2主成分は、第1主成分で表現できなかった情報（第1主成分にデータを射影をすることによって失われた情報）をよりたくさん捉えようとするので、主成分同士はいつも直行することになります。
このフランスパンの形をした２次元のデータの例では二つの主成分でしたが、もっと次元の高いデータセットではそれまでの2本の主成分に直行する第3主成分、第4主成分あるいはそれ以上のものも見つけ出します。
ここまでをまとめると、主成分分析（PCA）は高次元のデータにおいてデータ全体のばらつき（分散と言います）が最大となる方向を見つけ出し、元の次元と同じかそれよりも低い次元の新しい部分空間へ射影する手法です。
主成分分析（PCA）を利用するコード
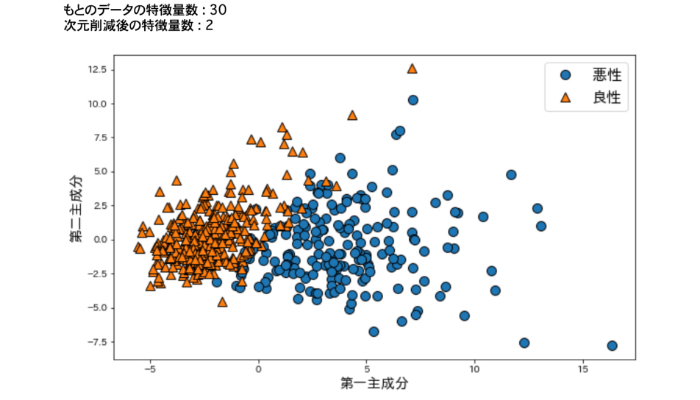
ここまで主成分分析（PCA）について整理をしてきましたが、イメージできたり理解できてたとしても使えなければ意味がありません。ここからは主成分分析（PCA）をコード（Python）を書いて実際に利用してみましょう。
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import mglearn
import japanize_matplotlib
#データをロードする
cancer = load_breast_cancer()
#データをStandardScalerでスケール変換し、個々の特徴量の分散が１になるようにする
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
#n_componentsに維持する主成分の数を指定し、データの最初の２つの主成分だけ維持する。
pca = PCA(n_components=2)
#fitメソッドを呼び出してcancerデータセットの主成分を見つける
pca.fit(X_scaled)
#最初の２つの主成分に対してデータポイントを変換。transformメソッドを用いてデータの回転と次元削減を行う
X_pca = pca.transform(X_scaled)
print(f"もとのデータの特徴量数 : {X_scaled.shape[1]}")
print(f"次元削減後の特徴量数 : {X_pca.shape[1]}")
#第１主成分と第２主成分によるプロットを行う。クラスごとに色分け
plt.figure(figsize=(10,6))
mglearn.discrete_scatter(X_pca[:,0],X_pca[:,1],cancer.target)
plt.legend(["悪性", "良性"],loc="best", fontsize=16)
plt.xlabel("第一主成分", fontsize=15)
plt.ylabel("第二主成分", fontsize=15)
plt.show()
＜補足 PCAオブジェクトを作る際にパラメータn_componentsに与える値について＞
- １より大きい数を指定した場合：返す特徴量の数を指定したことになる
- ０〜１の間の数を指定した場合：指定されただけの分散を維持できる最小数の特徴量を返す（普通この値には、0.95や0.99を指定。これで元の特徴量の95%もしくは99%の分散を維持できるように指定したことになる）
このように主成分分析（PCA）によって、30次元のデータを2次元に次元削減して可視化することができました。
ちなみに、主成分分析（PCA）がうまく機能するのは線形分離可能な問題に対してであって、線形分離不可能な問題に対してはカーネル主成分分析を使うのが良いとのこと。カーネル主成分分析についてはまた後日勉強していきたいです。
＜補足 線形分離可能と線形分離不可能＞
線形分離可能な問題のイメージ：直線で二種類のデータをうまく分類できる
線形分離不可能な問題のイメージ：直線では二種類のデータをうまく分類できない
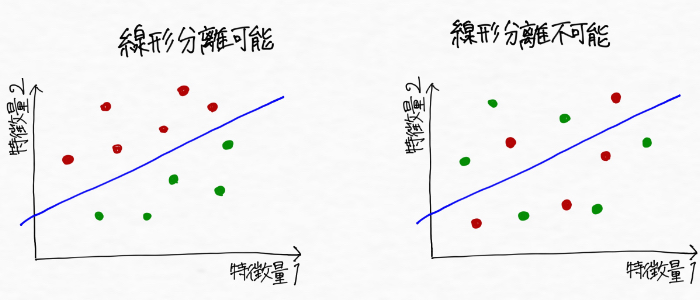
※これを一般化して、n次元空間上のふたつの点の集合をn-1次元の超平面で分離できることも線形分離可能と呼ぶ。逆に、分離できない場合を線形分離不可能と呼ぶ
まとめ
さて、今回は教師なし学習の基本から始まり主成分分析（PCA）による次元削減について理解を深めてきました。振り返ってみると、
- 教師なし学習にはクラスタリングと次元削減がある
- 次元削減はデータの次元を下げる処理のことを言い、高次元のデータセットを可視化したり、教師あり学習のアルゴリズム精度向上に貢献、メモリ使用量や計算時間を削減できるなどの効果がある
- 主成分分析は、最も分散が大きくなる方向である主成分に対してデータを射影することで元の次元よりもデータを削減していく方法である
ということがわかりました。
本記事では専門的な内容を扱っているので、この記事を読んでくださっている方にはAI（機械学習）を実務で活用しようとされている方が多いのかもしれません。僕自身AI会社をクビになりながらもAI（機械学習）エンジニアになることを目指して日々機械学習の学びを進めていますが、教師なし学習である主成分分析（PCA）とクラスタリング（以前整理しました）を理解して一気に前へ進めました！（・・・気がする）
というのは、今までは他人の機械学習プログラミングのコードを読んでいても「なんでこの処理するの？」の連発だった状態が、教師なし学習を学んだ今では「だからこの処理をしているのか！」と納得して腹に落とし込める体験がとても増えたからです。
ただ、世間で高く評価を受けている書籍を読んで理解できないなど、教師なし学習を学ぶ際には非常に苦労しました(´；ω；`)。。そんな時には参考にする書籍やWebページを変えてみたりすると理解が深まったので、諦めず様々な情報源に当たることの大切さも今回記事を作りながら実感しています。
先日そうした気づいたことを記事にしてみたので興味のある方はどうぞ
今回の教師なし学習をはじめとして、専門的な内容は時に理解できなくてくじけそうな時もありますが、理解できればとても楽しくなるものなのでゆっくりとでも自分のペースで理解を深めていきたいですね！
＜参考＞
AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。
コメントをどうぞ