AI（人工知能）を実現する技術である機械学習(※)を学んでいると、「機械学習はデータが命！データの品質と有益な情報の量で性能が決まる！」とはよく聞くもので、いかに優れたデータを作るかが機械学習エンジニアの腕の見せどころだと言われています。特徴量（データにどのような特徴があるかを数値で表現したもの）を抽出する作業は「特徴量エンジニアリング」と呼ばれますが、機械学習に関心のある方ならとても興味があることでしょう。
実際、元Google BrainやBaidu AIのリーダーでありその他の素晴らしい活動から著名なAndrew Ng氏も2013年に公開したレポートの中で
「機械学習の実践」とは、つまるところ特徴量エンジニアリングを行うことである
と述べているほど、特徴量エンジニアリングは非常に重要です。
機械学習プロフェッショナルたちの技を無料で見てKaggle(※)で、特徴量エンジニアリングについて学んでいる人も多いことでしょうが僕もそのうちの一人です。しかし、特徴量エンジニアリングの基本的なことさえ理解できていないのが僕の実際のところです 汗
そこで今回は機械学習エンジニアの奥義（勝手にそう呼んでます）特徴量エンジニアリングについて調べ理解を深めることでレベルアップに繋げることにしました！！
—————補足—————
※機械学習：AI（人工知能）を実現する技術の一つ。データからそのデータに潜むパターンや傾向を見つけ、見つけたパターンや傾向を元に未知のデータに対しても判定や予測を行っていく技術
※特徴量：求めたいものを特徴づけるもののことです。例えば、機械学習を利用して天気データから飲食店の売上を予測したい場合、天気や気温、湿度などの売上に寄与する情報は売上げを予測するために必要な特徴量と言う
※Kaggle：世界中のデータサイエンス・機械学習に携わる人が参加するコミュニティーサイト。世界中の企業から提供されているデータを機械学習を利用してデータ分析の腕を競い合う。機械学習のプロたちの知見を誰でも無料で得られる
———————————
特徴量エンジニアリングができないと痛い目にあう
ヘナチョコレベルな僕ですから過去に能力不足で悔しい体験もありました。僕が実力不足でクビになった前職、AI開発会社お多福ラボにて一日中Kaggleをやる活動に参加していた時のことです。
今日一日Kaggleに取り組んで学んだことを1人ずつ発表していこうか。
＜和泉さんってこんな人＞
常に頭の回転が早い、論理の鬼のような人。冷静沈着厳しいことをさらっと言う、AI開発会社「お多福ラボ」の役員。和泉さんから以前クビの宣告を頂いて今はAIZINEのライターやってます 汗
※登場人物紹介はこちら
メンバーの各々が学んだことを発表する中で僕は、、、
コードの意味がわからずに関数調べたりしてて1日が終わってしまいました
・・・・。技能不足でついて来れないならKaggleを業務中するのは認められない。土屋さん（つっちー）は参加しないでほしい。
その体験を思い出すとやっぱり悔しいですし、もっとレベルアップをしたいわけです。こうした背景もあって、今回は機械学習エンジニアの奥義（僕が勝手にそう呼んでます）特徴量エンジニアリングについて調べて理解を深めることにしました。
カテゴリ変数を連続値に変換する
まずそもそものところから知識を整理していきますが、データには様々な種類がある一方で多くの機械学習ライブラリ(※)では入力されるデータは数値しか受け入れません。そのため数値型でないデータは機械学習ライブラリに渡す前に数値で表現できるように処理をしてやる必要があります。
一般的な特徴量の種類として
- 売上や花の大きさの測定値などの「連続値特徴量(※)」
- 製品名や色などの「カテゴリ特徴量（離散値特徴量）(※)」
がありますが、多くの場合カテゴリ特徴量は数値ではありません。そこでカテゴリ特徴量の処理がポイントになってくるわけですね。
—————補足—————
※ライブラリ：再利用できるプログラムを集めたもので、多くの場合は単体では動かず主のプログラムの実行を補助する
※連続値・・・1.1や1.01のように繋がった値をとれるもののこと。時間や速度など
※離散値・・・連続値とは異なり、間の値を取ることができないものを離散値と言います。例えばコイン投げの回数は、表1.2回、裏1.8回とは表現できません。
———————————
0と１で表現し直すワンホットエンコーディング（one-hot encoding）
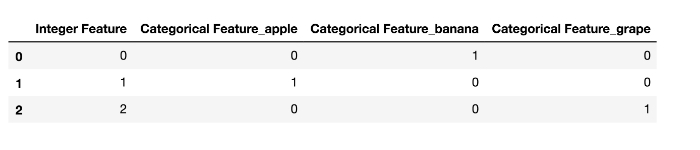
調べてみると、カテゴリ変数を表現する方法としてはワンホットエンコーディング（one-hot encoding）と呼ばれる手法がよく用いられています。これは、例えば「リンゴ」とか「バナナ」という情報があった時にそれらを０と１で表現する手法です。・・・なんのこっちゃ？ということですが、具体的にはカテゴリ特徴量を次のように０と１の値を持つ新しい特徴量で表現し直す方法です。
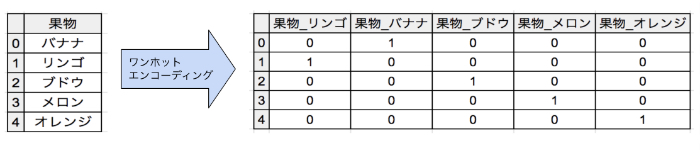
またカテゴリ変数が整数として表現されている場合もあるので注意しなければなりません。どういうことかと言えば例えば、次のように元々のデータでバナナが「１」、リンゴが「２」、ブドウが「３」・・・というように表現されていた場合、
「これは整数だからそのまま機械学習ライブラリに渡しちゃえ！わーい( ´∀｀)」
としてしまうと、機械学習ライブラリは与えられたデータを連続値特徴量として認識捉えるため、「ほうほう、バナナはリンゴより小さく、リンゴはブドウよりも小さいんだな、ふむふむ」なんていう、おかしな判断をしてしまいます。
そのため、機械学習モデルに正しくデータの特徴を掴んでもらうために、データの種類に配慮して特徴量が連続値特徴量なのかカテゴリカル特徴量なのかを見極めることがめちゃ大事！！というわけですね。
ワンホットエンコーディングは次のように実行できます。
import pandas as pd
#整数特徴量とカテゴリカル文字列特徴量からなるDataFrameを作る
demo_df = pd.DataFrame({'Integer Feature':[0,1,2],'Categorical Feature':['banana','apple','grape']})
demo_df
#Integer Feature列に対してもワンホットエンコーディングを適用したい場合はcolumnsパラメータで指定する pd.get_dummies(demo_df, columns=['Integer Feature', 'Categorical Feature'])
ビン番号を新たな特徴量とする離散化（ビニング）
次は新たな特徴量を実際に作成して機械学習モデルの性能を高めていく方法について見ていきましょう。
まず、線形モデル(※)を連続値のデータに対してより強力にする方法の一つとして特徴量の「離散化（ビニング）」があります。これは特徴量を次に述べる方法で複数の特徴量に分割する方法で、特徴量の入力範囲を等間隔の区間（ビンと呼ぶ）に区切り、個々のデータポイントがどのビンに入るかを表現したカテゴリ特徴量に置き換えるという手法です。
※線形モデル：y=w0x0 + w1x1 + w2x2 + ・・・wmxmで表現されるモデル。もっと詳しく知りたい方はこちら
文字にするとややこしく感じてしまいがちですが、何も難しいことはありません。例えば次のようにデータポイントを等間隔に10区間に区切って、それぞれのデータポイントにどのビン（区間）に入るかを表す1〜10いずれかの番号を割り振ります。
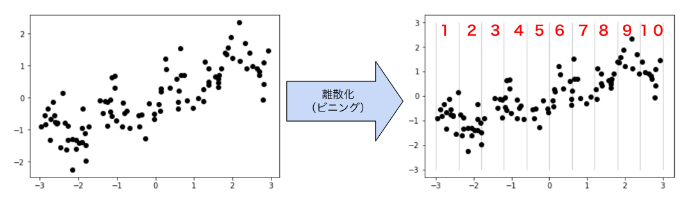
つまり上図を参考にすれば、離散化（ビニング）をすることで例えば
1.04, 0.16, 2.99,・・・というデータが
７, ６, 10,・・・ というように各データポイントに1~10の番号を割り当てて表現できるわけです。
これは言い換えれば元々一つだった単一の特徴量を、個々のデータポイントがどこに入っているか（1〜10のどのビンに入っているか）を表現したカテゴリ特徴量へ置き換えたということですね。
例えるなら、一つのリンゴの味見をしてリンゴを評価したい時に、お母さんがリンゴを切って、「この一切れは◯◯ちゃんに味見してもらいましょう」「この一切れは◯◯君に味見してもらいましょう」・・・と10人分に割り当てることで一つのリンゴから得られる情報の量を増やした、ということです。（例えが微妙かもしれませんけど）
ただし、1〜10のどのビンに入っているかを表現した番号は整数ですがカテゴリ特徴量です。なので、これら10個のカテゴリ特徴量に対して続いてワンホットエンコーディングを実施すれば、元は一つだった特徴量を10個にして機械学習ライブラリに渡せるってわけですね。（なるほど！）
ここで早速、離散化（ビニング）を使って作成した特徴量がどういう効果をもたらすか具体的に確認してみましょう。ちなみに機械学習モデル(※)ごとに最適な特徴量というのは異なるため、自分が使おうとしている機械学習モデルにとって、作成した特徴量が有効かどうかは試してみるまでわかりません。
青リンゴが好きな人、赤リンゴが好きな人と人それぞれ好みが違うように、機械学習モデルにも好みがあるんですね(^^)
今回は線形回帰モデルと決定木モデル(※)を使ってチャレンジです！
—————補足—————
※モデル：事象を簡単にして本質（データのパターンやルール）を数式で表したもの
※決定木：機械学習アルゴリズムの一つで一連の質問に基づいて決断を下す方法でデータを分類していきます
————————————
試してみるのは、次のようにデータがあったときに、
離散化（ビニング）を行わずに線形回帰と決定木を実施した場合と、離散化（ビニング）を行って次のようにデータを10区間に分割してビン番号（どこに入るかを表現した数）のカテゴリ特徴量に置き換えた上で線形回帰と決定木を実施した場合です。
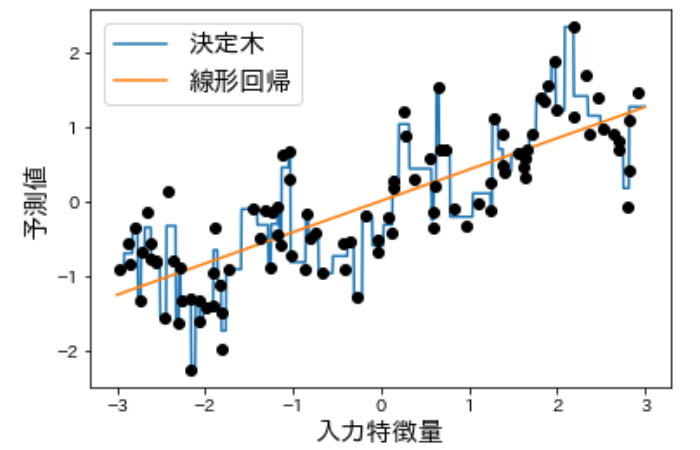
まずは元のデータに対して線形回帰と決定木を用いて次のようにモデルを訓練させてみます。
以下のように結果が出ました。
一方、離散化（ビニング）を行った後のデータに対して線形回帰と決定木を用いてモデルを訓練させてみると、
次のように結果が出ました。
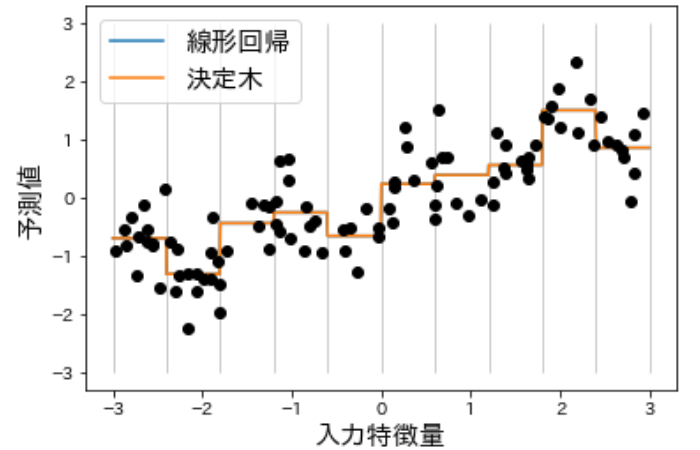
（すごい、、線形回帰こんなに変わるんだ。。。）と、このように離散化（ビニング）によって線形モデルがデータに対してより柔軟になっていることがわかります（線形回帰の結果と決定木の結果が完全に重なっています）。ビンごとに値が一定になっていますが、これは考えてみればワンホットエンコーディングで0と1の表現にしてビン毎に特徴量の値が一定になっているので納得ですね。
一方で決定木は柔軟性が低下しているではありませんか！！一般的に複数の特徴量を同時に扱うことができる決定木にとって、一つの特徴量ごとにしか行えない離散化（ビニング）をすることはメリットがないようで、それはもともと決定木がデータを任意の場所で分割して学習できる（ビニングが最も有効な場合を自動的に学習している）からです。
以上を踏まえると、データがとても大きくて高次元な場合などどうしても線形モデルを使いたい時にいくつかの特徴量が出力と非線形な関係を持つようなら、離散化（ビニング）を使ってみると良いようです。
交互作用特徴量と多項式特徴量を加える 〜特徴量の2乗や特徴量同士の積〜
離散化（ビニング）に続いて特徴量表現をより豊かにする他の方法として、特に線形モデルに有効なものが元のデータの多項式特徴量と交互作用特徴量を加える方法です。
聞きなれない言葉が出てきたので順番に整理していきましょう。まず多項式特徴量とは、ある特徴量xに対してxを二乗、三乗、・・・して作った特徴量で、一方交互作用特徴量とは、特徴量A × 特徴量Bのように複数の特徴量の積で作られる特徴量です。
例えば、「恋人の有無」と「複数人の異性との肉体関係」と「バッシング」見てみると、恋人無しの人は、複数人の異性と肉体関係を持ってもバッシングされにくいですが、恋人有りの人は恋人無しの人よりも何かとバッシングを受けやすく、その中でも複数人の異性と関係の多い人の方がバッシングのリスクが高まるという見方があります。このように、2つ以上の要因が考えられる時、要因が組み合わさった時にだけ現れる作用のことを交互作用と言います。
※決して僕の意見を述べたものではなく、あくまで補足の例として出しています。この例えも微妙かもしれませんが。。。
さて、交互作用特徴量と多項式特徴量の効果をみていきましょう。交互作用特徴量と多項式特徴量はpreprocessingモジュールのPolynomialFeaturesを用いて次のように加えることができます。
コードの実行結果を見ると、
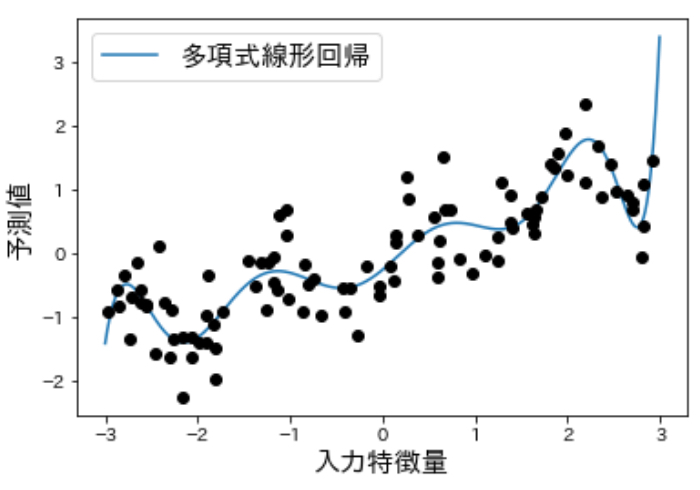
多項式を加えたことで、線形回帰の柔軟性が上がってデータの表現力が高まっていることがわかりますね！
ここまで同じデータばかりを扱ってきたので、ここからは他のデータについても交互作用特徴量と多項式特徴量を加える効果を見てみます。boston_housingデータセットに対して次のように交互作用特徴量と多項式特徴量を適用してみます。
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
#bostonデータセットを使用するためにロードする
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=0)
#データのスケール変換
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
#preprocessingモジュールのPolynomialFeaturesを用いて交互作用特徴量を抽出する
#2字までの多項式特徴量と交互作用を抽出する
poly = PolynomialFeatures(degree=2).fit(X_train_scaled)
X_train_poly = poly.transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)
#Ridgeを使って多項式特徴量、交互作用特徴量を入れた場合と入れない場合を比較する
ridge = Ridge().fit(X_train_scaled, y_train)
print(f"X_train.shape : {X_train.shape}")
print(f"Score with Original features : {ridge.score(X_test_scaled, y_test):.3f}")
print('-'*50)
ridge = Ridge().fit(X_train_poly, y_train)
print(f"X_train_poly.shape : {X_train_poly.shape}")
print(f'Score with polynomial features : {ridge.score(X_test_poly, y_test):.3f}')
print('-'*50)
#追加した特徴量を表示してみる
print(f"features : \n{poly.get_feature_names()}")
出力された結果を見ると、もともと13個の特徴量だったのが105個の特徴量となっていてスコアも上がっていますね！新しく作成した特徴量の中身を確認して見ると、元の特徴量の2つの全ての組み合わせと、元の特徴量の２乗になっていることがわかります。
このように特徴量を2乗、3乗したものを新たな特徴量として加えることが線形回帰モデルでは有用であるようですが、こうした交互作用特徴量と多項式特徴量を入れるとランダムフォレストのような複雑な機械学習モデルでは、わずかに性能が下がるようです。決定木ベースのモデルは、自分で重要な交互作用を見つけることができるので、多くの場合データを明示的に変換する必要はありません。
一方でSVM、最近傍法、ニューラルネットワークは、離散化（ビニング）、多項式、交互作用の恩恵を受けることがありますが、線形モデルの場合ほど大きなものでは無いようです。
数学関数で形を変えちゃう単変量非線形変換
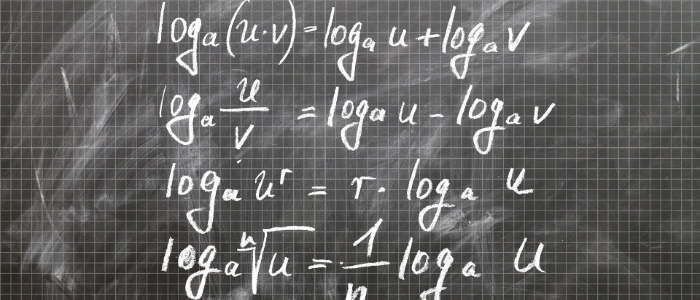
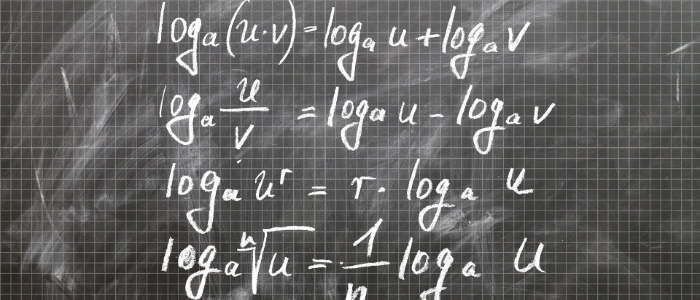
特徴量を２乗、３乗したものが、線形回帰モデルで有用であることを見てきましたが、他にlog、exp、sinなどの数学関数を用いた特徴量の変換が線形モデルやニューラルネットワークモデルに効果的です。
これはなぜ？？
・・・と僕自身思ったのですが、次の理由がありました。ほとんどの機械学習モデルは個々の特徴量がだいたい正規分布（ガウス分布）(※)に従っているときに最も上手く機能するという前提があり、こうした数学関数は特徴量を正規分布に近づけてくれる！！という訳なんですね。（なるほど！！）
※正規分布：データの分布が平均値を頂点とした左右対称の山形で表示される分布
不恰好なおにぎりをおにぎりケースに入れてフリフリすると綺麗に形が整ったおにぎりが出てきますが、数学関数はデータの分布について形を整えてくれるので、こうしたおにぎりケースのような存在と言えるかもしれません。
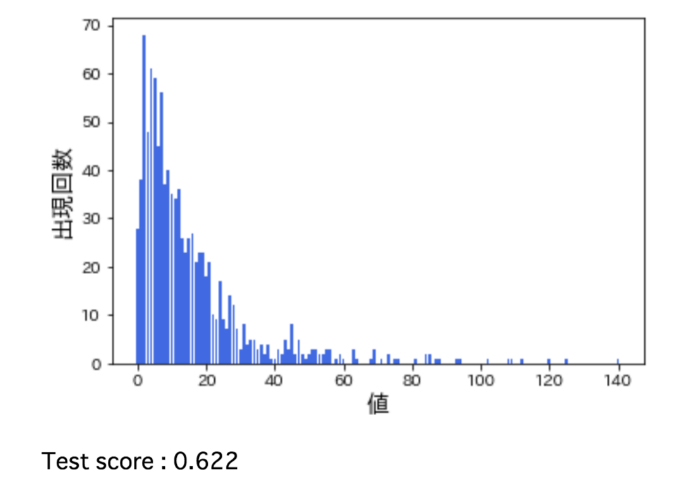
さて、数学関数を用いた特徴量の変換の効果については言葉だけでもわかりにくいですし、百聞は一見に如かずなので早速データを触って見てみます。下図はこれから扱うデータの分布を表していますが、一桁の小さな値が多い一方で 100を超える値も存在していることがわかります。
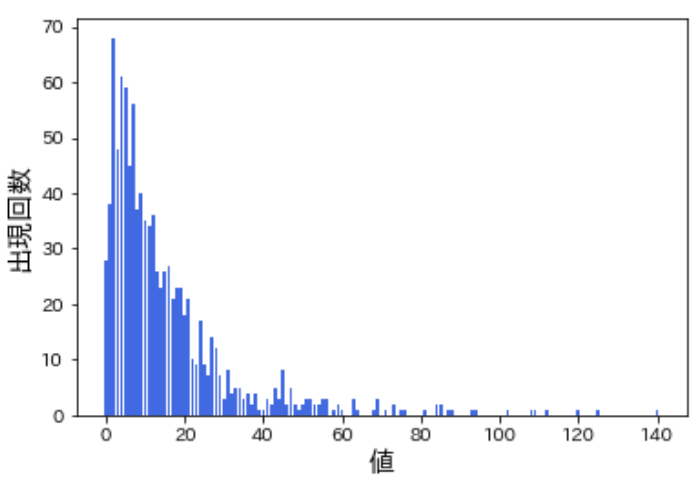
予測したいターゲット変数がこのように小さい値が多い一方でとても大きな値も存在する分布をしている時、多くの線形モデルはうまく機能しません。というのは正規分布に従っていないからです。
実際に次のようにリッジ回帰(※)で学習を行ってみると、R2は0.622となりました。
次はこのデータに対して対数変換を行うとどうなるかを見ていきましょう。データに0が含まれており、対数は0に対して定義できないのでlog(X+1)で対数変換を行います。次のようにして対数変換を行ない、その後のデータの分布とリッジ回帰に対するR2スコアを確認してみると、、
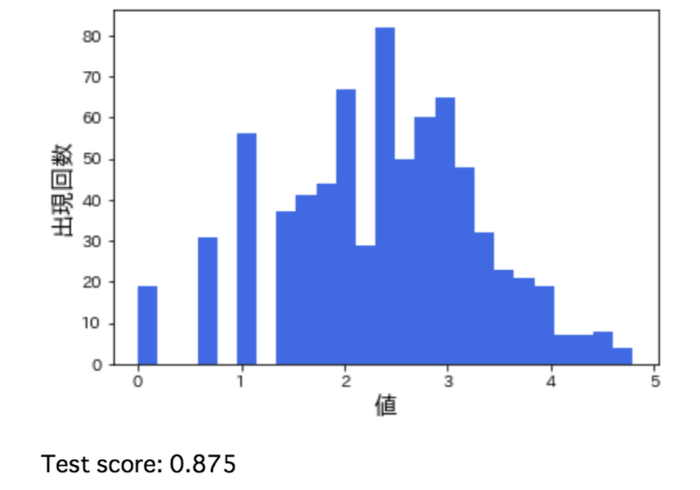
このように元のデータに比べて対数変換後のデータはずっと正規分布に近づいていますし、R2が高まっていることからリッジ回帰の性能が良くなっていることがはっきりとわかりますね！！
ここまで見てきたようにlog、expなどの関数が特に有効なのは、予測したいターゲット変数のとる値が1、10、100などのように複数の桁に渡って分布していて、正規分布に従っていない場合です。ちなみに、sin、cos関数は周期的なパターンを持つ関数を扱う際に有用みたいです。
—————補足—————
※リッジ回帰：正則化された線形回帰の一つで、線形回帰に「学習した重みの二乗の合計（L2正則化項）」を加えたもの。もっと詳しく知りたい方はこちら
※R2：決定係数。回帰によって導いたモデルの当てはまりの良さを表現する値で、モデルによって予測した値が実際の値とどの程度一致しているかを判断する評価指標。もっと詳しく知りたい方はこちら
———————————
自動特徴量選択でいらない特徴量はポイポイ捨てたい
特徴量を多く追加すると、モデルは複雑になり、訓練データに対してしか高い性能を発揮できないという困った状況である過学習に陥る可能性が高くなります。残念ながら追加すればするほど良い！というわけではありません。
※過学習については以前整理しましたので、興味のある方はご参考ください
そのため、新しい特徴量を加える場合や高次元のデータセットを扱う場合には、最も有用な特徴量だけを残して残りを捨てて特徴量の数を減らす（次元削減）のは良い考えだと言われています。なぜなら次元削減をすることでモデルが単純になって解釈しやすくなるだけでなく、汎化性能が向上するからです。
さらに特徴量が少なくなった分計算コストが下がって計算時間が短縮できたり、高次元のデータによってパフォーマンスが下がる「次元の呪い」と呼ばれる現象を防ぐなどのメリットも！！
これはちょうど植物の剪定に似ているかもしれません。枝や葉っぱが多ければ多いほど良い訳ではないからです。不必要な枝や葉を取り除けば、植物が吸い上げた栄養を適切な箇所に集中して行き渡るようになって成長が促進しますし、見た目も美しく且つ普段の手入れもしやすくなります。
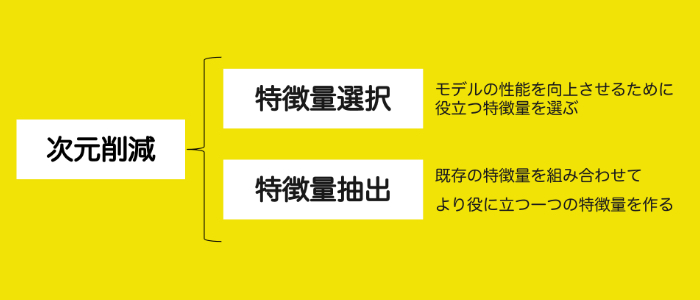
こうした様々なメリットを持つ次元削減には「特徴量選択」と「特徴量抽出」がありますが、前者の「特徴量選択」はモデルの性能を向上させるために役立つ特徴量を選ぶ方法で、この方法はとりわけ正則化(※)されていないモデルに役立ちます。一方「特徴量抽出」は既存の特徴量を組み合わせてより役に立つ一つの特徴量を作る方法です。
※正則化：簡単に言うと数式で表されるモデルに「正則化項」と呼ばれるものを罰則として足し算することで、モデルの形が複雑になりすぎないように調整しようというものです
特徴抽出の代表的な手法の主成分分析（PCA）については以前まとめていますので興味のある方はどうぞ
特徴量選択と特徴量エンジニアリングは厳密には別物なのかもしれませんが、機械学習モデルの性能を上げるという意味では同じ目的を持っていると考えて今回一緒に整理してみました。
今回は「特徴量選択」に焦点を当てて理解を深めていきます。
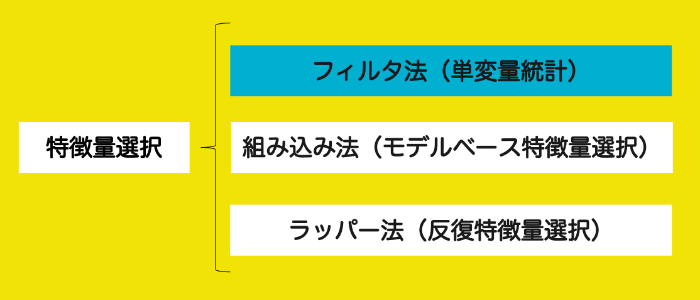
「特徴量選択」は大まかに
- フィルタ法（単変量統計）
- 組み込み法（モデルベース特徴量選択）
- ラッパー法（反復特徴量選択）
と呼ばれる3つのタイプがありますので一つずつ整理していきましょう。
処理は早いが精度が低くなりがち！フィルタ法（単変量統計）
フィルタ法（単変量特徴量選択）は、機械学習を伴わずに特徴量の重要度を測定して有効な特徴量を選択する手法です。個々の特徴量とターゲット（目的変数）との間に統計的に顕著な関係があるかどうかを計算し、最も高い確信度で関連している特徴量が選択されます。各特徴量について、使うべきか捨てるべきかを判断する方法は、特徴量とターゲット（目的変数）のデータ型によって変わってくるようです。
- 特徴量が多すぎてモデルを作ることができないような場合や、多くの特徴量が全く関係ないと思われるような場合には有効
- 個々の特徴量を個別に考慮するため他の特徴量と組み合わさって意味を持つような特徴量は捨てられてしまう
- 多くの機械学習モデルに対して有効で処理が早いが精度は低くなる
フィルタ法（単変量特徴量選択）はSelectKBestを用いて次のようにして実行できます。
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectPercentile, f_classif
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
#cancerデータセットを使用するためにロードする
cancer = load_breast_cancer()
#シードを指定して乱数を生成する
rng = np.random.RandomState(42)
#numpy.random.normal()を用いて正規分布に従う乱数を出力する
noise = rng.normal(size= (len(cancer.data), 50))
#フィルタ法によってノイズが取り除かれてモデルの性能が高まることを期待して、ノイズ特徴量をデータに加えておく
#最初の30特徴量はデータセットから来たもので、続く50の特徴量はノイズである。
X_w_noise = np.hstack([cancer.data, noise])
#trainデータとtestデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X_w_noise, cancer.target, random_state=0, test_size=.5)
#SelectPercentileを使って50%の特徴量を選択。分類の場合はf_classifを用いる（回帰にはf_regressionを用いる）
select = SelectPercentile(score_func=f_classif, percentile=50)
select.fit(X_train, y_train)
#trainデータとtestデータを変換
X_train_selected = select.transform(X_train)
X_test_selected = select.transform(X_test)
#ロジスティック回帰の学習
lr = LogisticRegression()
#変換前のデータを用いた結果
lr.fit(X_train, y_train)
print(f"X_train.shape : {X_train.shape}")
print(f"Score with all features : {lr.score(X_test, y_test):.3f}")
print('-'*50)
#変換後のデータを用いた結果
lr.fit(X_train_selected, y_train)
print(f"X_train_selected.shape : {X_train_selected.shape}")
print(f"Score with only selected features : {lr.score(X_test_selected, y_test):.3f}")
コードの出力結果を確認すると、全ての特徴量を使った場合とフィルタ法（単変量統計）を行った上で使った場合とでは後者の場合の方がロジスティック回帰の性能が確かに向上していますね！！
交互作用を捉えられる！組み込み法（モデルベース特徴量選択）
続いて組み込み法（モデルベース特徴量選択）は、教師あり機械学習モデルを使って個々の特徴量を判断して重要なものだけを残す手法です。フィルタ法（単変量選択）の場合とは対象的に組み込み法（モデルベース特徴量選択）は全ての特徴量を同時に考慮するので、選択に使うモデルが交互作用を捉えられるなら特徴量同士の交互作用を捉えることができます。
※組み込み法は参考書によっては埋め込み法と表記されています
組み込み法（モデルベース特徴量選択）に用いるモデルは最終的に使う教師あり学習モデルと違っていても良いのですが、選択時に特徴量に順番をつけるために個々の特徴量の重要性の指標を出力するものでなければなりません。例えば、決定木や決定木ベースモデル、Lasso回帰（ラッソ回帰）、線形モデルなどがよく使用されるようです。
重要でない特徴量の係数を0にしてくれるLasso回帰と、線形回帰ついては以前整理したことがありますので興味のある方はこちらをご覧ください。
- 決定木や決定木ベースモデルには特徴量の重要性そのものをエンコードしたfeature_importances_属性がある。線形モデルには係数があり、これも絶対値をとれば特徴量の重要性を捉えた値として利用できる
- ワンホットエンコーディングされたカテゴリ特徴量は、特徴量の重要性がエンコード後の2値変数（０と１）に分散してしまう
- 互いに強く相関した2つの特徴量がある場合、これらの特徴量の重要性は2つの特徴量に均等に配分される訳ではなく一方の特徴量に集中してしまう
組み込み法（モデルベース特徴量選択）は次のように利用できます。
#組み込み法（モデルベース特徴量選択）
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
#cancerデータセットを使用するためにロードする
cancer = load_breast_cancer()
#シードを指定して乱数を生成する
rng = np.random.RandomState(42)
#numpy.random.normal()を用いて正規分布に従う乱数を出力する
noise = rng.normal(size= (len(cancer.data), 50))
#フィルタ法によってノイズが取り除かれてモデルの性能が高まることを期待して、ノイズ特徴量をデータに加えておく
#最初の30特徴量はデータセットから来たもので、続く50の特徴量はノイズである。
X_w_noise = np.hstack([cancer.data, noise])
#trainデータとtestデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X_w_noise, cancer.target, random_state=0, test_size=.5)
#組み込み法（モデルベース特徴量選択）を用いるには、SelectFromModelを用いる
#指定したスレッショルド（閾値）よりも大きい特徴量だけを選択する
select = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=42), threshold="median")
select.fit(X_train, y_train)
X_train_selected = select.transform(X_train)
X_test_selected = select.transform(X_test)
#組み込み法（モデルベース特徴量選択）を用いていない結果
score_pre = LogisticRegression().fit(X_train, y_train).score(X_test, y_test)
print(f"X_train.shape : {X_train.shape}")
print(f"Test score : {score_pre:.3f}")
print('-'*50)
#組み込み法（モデルベース特徴量選択）用いた結果
score = LogisticRegression().fit(X_train_selected, y_train).score(X_test_selected, y_test)
print(f"X_train_l1.shape : {X_train_selected.shape}")
print(f'Score with only selected features : {score:.3f}')
コードの処理結果を見ると、全ての特徴量を使った場合と続いて組み込み法（モデルベース特徴量選択）を行った上で使った場合とでは後者の場合の方がロジスティック回帰の性能が確かに向上していますね！！
計算コストは大きいが品質は高い！反復特徴量選択（ラッパー法）
ラッパー法（反復特徴量選択）は学習を行いながら重要な特徴量を選択する手法です。ラッパー法（反復特徴量選択）には、次の二つの方法があります。
- 後退法：全く特徴量を使わないところからある基準が満たされるところまで1つずつ特徴量を加えていく方法
- 前進法：全ての特徴量を使う状態から1つずつ特徴量を取り除いていく方法
そしてラッパー法（反復特徴量選択）の一つが再帰的特徴量削減（recursive feature elimination：RFE）で、RFEは全ての特徴量から開始してモデルを作成しそのモデルで最も重要度が低い特徴量を削減します。そしてまたモデルを作って最も重要度が低い特徴量を削減します。この過程を事前に定めた数の特徴量になるまで繰り返します。
ラッパー法（反復特徴量選択）が機能するためには、モデルベース選択の場合と同様に、選択に用いるモデルが特徴量の重要性を決定する方法を提供していなければなりません。
- 多数のモデルを作るため、計算量が非常に大きくなる
- どの特徴量を入力として使ったらいいかわからない場合に使える
- 予測を高速化したい場合や解釈しやすいモデルを構築したい場合などに、必要な特徴量の量を減らすためにも役立つ
- フィルタ法（単変量統計）よりも過学習が起きやすい
ラッパー法（反復特徴量選択）を実際に行ってみると次のようになります。
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
#cancerデータセットを使用するためにロードする
cancer = load_breast_cancer()
#シードを指定して乱数を生成する
rng = np.random.RandomState(42)
#numpy.random.normal()を用いて正規分布に従う乱数を出力する
noise = rng.normal(size= (len(cancer.data), 50))
#フィルタ法によってノイズが取り除かれてモデルの性能が高まることを期待して、ノイズ特徴量をデータに加えておく
#最初の30特徴量はデータセットから来たもので、続く50の特徴量はノイズである。
X_w_noise = np.hstack([cancer.data, noise])
#trainデータとtestデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X_w_noise, cancer.target, random_state=0, test_size=.5)
select = RFE(RandomForestClassifier(n_estimators=100, random_state=42), n_features_to_select=40)
select.fit(X_train, y_train)
X_train_rfe = select.transform(X_train)
X_test_rfe = select.transform(X_test)
#RFEを用いていない場合のスコア
score = LogisticRegression().fit(X_train, y_train).score(X_test, y_test)
print(f"X_train.shape : {X_train.shape}")
print(f'Test score : {score:.3f}')
print('-'*50)
#RFEを用いて選択した特徴量を用いた場合のスコア
score = LogisticRegression().fit(X_train_rfe, y_train).score(X_test_rfe, y_test)
print(f"X_train_rfe.shape : {X_train_rfe.shape}")
print(f'Score with only selected features : {score:.3f}')
コードの処理結果を見ると、RFEを用いて特徴量選択を行ったロジスティック回帰モデルの方が性能が高くなっていることがわかりますね！
強力な特徴量を作るには専門家知識の利用が効く！
特徴量エンジニアリングでは、専門家しか知らない知識、つまりある事象に昔から関わっている人の知識を利用することがとても効果的です。これらはそのまま専門家知識と読んだり、ドメイン知識（domain knowledge）と読んだりするようで、ある領域の専門家が元々のデータから得られる特徴量よりもはるかに情報量の多い有用な特徴量を特定する手助けになることがよくあります（あるみたいです）。
要は、目的変数を予測するのに有効活用できそうな特徴量を作るために、その領域に詳しい人の視点や専門家の知識を活用すると良い！ということですね！
例えば、機械学習を用いてある国における食品Aの毎月の売上を予測したいとした場合、「毎週水曜日には断食の習慣がある」だったり「この時期には消費を控える慣習がある」というような細かな知識を持っていれば、その情報（特徴量）を利用することでより正確な売上予測ができるようになります。
専門家知識を用いて作った特徴量は 非常に強力で、平均値など汎用的な方法で作った特徴量はそうした特徴量を考えるためのヒントや補助として使う方が多いようです。
まとめ
さて今回はレベルアップのために機械学習エンジニアの奥義である特徴量エンジニアリングに理解を深めてきました。
振り返ってみると、機械学習は全てを連続値として受け入れるので、データの種類に配慮して特徴量が連続値特徴量なのか、カテゴリカル特徴量なのかを見極めが大事でした。また、線形モデルに効果的な特徴量エンジニアリングの手法として、一つの特徴量を分割してビン番号を新たな特徴量とする離散化（ビニング）や、元の特徴量を利用して作成した交互作用特徴量や多項式特徴量を加えること、さらにlogなどの数学関数を用いた特徴量の変換も効果的でした！
こうした手法を用いて特徴量を追加すればすれば良いという訳ではなく、本当に重要な特徴量だけを選択することも忘れてはいけません。
機械学習を伴わずに特徴量の重要度を測定して有効な特徴量を選択するフィルタ法（単変量特徴量選択）、教師あり機械学習モデルを使って個々の特徴量を判断して重要なものだけを残す組み込み法（モデルベース特徴量選択）、そして学習を行いながら重要な特徴量を選択するラッパー法（反復特徴量選択）が効果的でした。
このような手法に加えて、専門家知識を利用することで強力な特徴量を得られるということも押さえておきたいポイントでしたね！！
・・・と、今回もめちゃくちゃ盛りだくさん & 長くなってしまいました。。。(°▽°)
改めて機械学習が上手くいくかどうかを決定する重要な要素は、どのような特徴量を用いるか、どの特徴量とどの機械学習手法を組み合わせて用いるかであることは間違いありません。
特徴量エンジニアリングにはたくさんのやり方があって機械学習分野の勉強に決して終わりはないです。
学ぶことが多すぎて毎回すごい世界に足踏み入れたなあと感じてます。
常に新しい情報をインプットし続ける必要があるエンジニアという職業は知的好奇心の強い人じゃないと務まらないですし、実際にエンジニアとして活動されている方は本当にすごいなあと思います。（僕もそこを目指しているんですけど。。）
ちなみに、特徴量エンジニアリングと関わりの深いデータの前処理についても整理していますので興味のある方はこちらからどうぞ
今回学んだことを基礎知識として活用しながらどんどんKaggleなどで手法を実践、技を磨いていきたいですね！
＜参考＞
続く↓
AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。
