超入門！リッジ回帰・Lasso回帰・Elastic Netの基本と特徴をサクッと理解！

AI（機械学習）を学び始めると「リッジ回帰」や「Lasso回帰」、「Elastic Net」なんていう小難しそうな単語を見かけますよね。こうした単語による処理はコード数行で実行できてしてしまいますが、中身を理解しておかないと使いこなせないのは当然のことでしょう。

そこで今回は「リッジ回帰」、「Lasso回帰」、「Elastic Net」の基本と特徴、これらがどのようなものであるかついてお伝えしていきます。

一言で言うと「リッジ回帰、Lasso回帰、Elastic Net」とは・・・

線形回帰と正則化

リッジ回帰を理解するために、まず「線形回帰」「正則化」「重み」「コスト関数」という言葉の意味を再確認していきましょう。

※既に理解されている方は本章読み飛ばしてください。

線形回帰

まず「線形回帰」とは、データがm個あるとした時にデータの傾向やパターンを上手く表現できる

y = w0 × x0　+　w1 × x1　+　w2 × x2　+・・・+　wm × xm

という数式（モデル）を見つけ出すことです。適切な線形回帰モデルを見つけ出せれば、未知のデータから売上や気温のような連続値を予測することが可能になります。説明変数が１つだけの線形モデルはy = w0　+　w1 × x という直線の形で表現されるので馴染みのある方も多いことでしょう。　

（もっと詳しく知りたい方はこちら↓）

線形回帰

「線形回帰」という単語はAI（機械学習）を学び始めた人ならば誰しも出会う言葉ですよね。しかし、コード一行で線形回帰の処理は完了してしまうので、具体的にどういうものであるかの理解が曖昧のままの人は意外に多いかもしれません。そこで今回は線形回帰についてお伝えしていきます。

aizine.ai

正則化

次に「正則化」とは、過学習を防いで汎化性能（未知のデータへの対応能力）を高めるためのテクニックの一つで、モデルに「正則化項」というものを付けることでモデルの形が複雑になりすぎないように調整しようとするものです。

具体的には、モデルの係数の絶対値または二乗値が大きくなってしまうと、訓練データのモデルに適合しすぎて、テストデータのモデルの当てはまりが悪くなる過学習という現象が起こるので、過学習を避けるために正則化項をつけています。

（もっと詳しく知りたい方はこちら↓）

AI（機械学習）でよくある問題過学習って？ゼロからわかる基本と対策

AI（機械学習）を実装しようとする際に誰もが直面する問題「過学習」。「過剰適合」や「オーバーフィッティング」とも呼ばれる現象ですが、過学習がなぜ起き、どういうもので、どう対策したらいいのか？について僕は理解できてません。そこで今回は、この過学習の詳しい内容や対策について調べて理解していきます！

aizine.ai

重み

そして「重み」とは、説明変数（求めたいものに作用する変数）が目的変数に与える影響度合いを表現したものです。例えば線形回帰モデルでいえばw1やw2など説明変数の係数が重みに当たります。「重み」は英語では「Weight」と表現されるので「重量」という意味をイメージしがちですが、ここでの「重み」は「大切さや価値、重要性」という意味を持っています。

コスト関数

最後にコスト関数とは、「構築したモデルがどれだけ悪いかを測定する関数」で、機械学習の分野ではコスト関数を最小化することがモデル構築の肝となります。

（線形回帰のコスト関数についてはこちら↓）

平均二乗誤差（MSE：Mean Square Error）

機械学習を学び始めると「平均二乗誤差（MSE：Mean Square Error）」という言葉によく出会いますよね。この単語は機械学習への苦手意識をグ〜ンと高めてしまいかねない単語でしょう。しかし、機械学習の知見を深めたい人は理解必須です。そこで今回は平均二乗誤差（MSE）についてお伝えしていきます。

aizine.ai

以上、ここまでは「線形回帰」「正則化」「重み」についての知識を整理してきました。次からはいよいよ「リッジ回帰」「Lasso回帰」「Elastic Net」について理解を深めていきます。

リッジ回帰

リッジ回帰は「正則化された線形回帰の一つで、線形回帰に「学習した重みの二乗（L2正則化項）」を加えたもの」です。

つまり、線形回帰のコスト関数（最小二乗コスト関数）に重みの平方和を足し合わせたものがリッジ回帰です。データがm個あるとすると線形回帰の学習した重みの二乗の合計は、w0^2 + w1^2 +・・・＋wm^2 で表現できます。「全部足し合わせをする」という意味の記号Σを用いて、リッジ回帰は次のように表現されます。

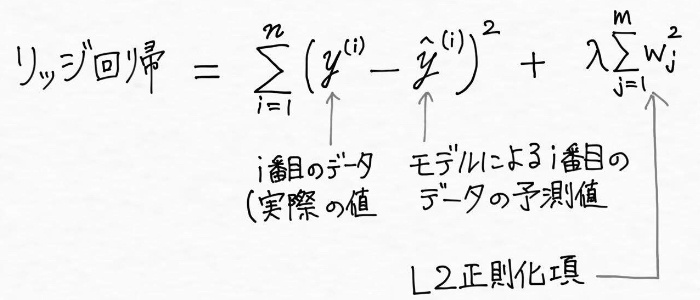
ハイパーパラメータλ（ラムダ）の値を増やすことでL2正則化項（L2ペナルティ）の値を大きくして正則化の強さを引き上げ、モデルの重みが小さくなるようにします。これは説明変数の影響が大きくなりすぎないように抑えているわけです。L2正則化項による正則化では重みは完全に０にはならない性質があるため、説明変数が非常に多い時にはモデルの解釈が複雑になるという欠点があります。

Lasso回帰

リッジ回帰と同じく正則化された線形回帰の一つがLasso回帰です。Lasso回帰は最小二乗コスト関数に対して、重みの合計を足したもの（L1正則化項と呼びます）で、データがm個あるとすると以下のように表現されます。

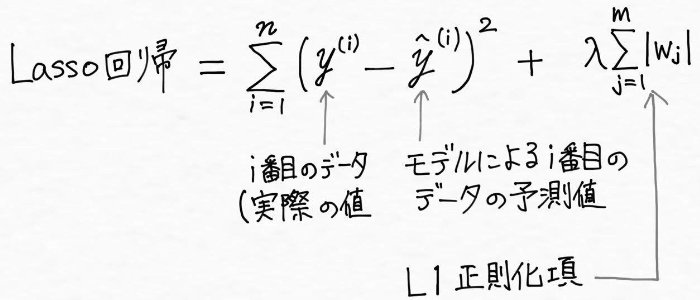
Lasso回帰はリッジ回帰と違って不要と判断される説明変数の係数（重み）が0になる性質があり、つまりモデル構築においていくつかの特徴量（説明変数）が完全に無視されるということです。言い換えれば、モデルの選択と同時に説明変数の数を削減して、説明変数（特徴量）の選択を自動で行ってくれるとも言えます。

つっちー

＜もっと詳しく知りたい方へ＞

リッジ回帰では重みが０にならないけれどLasso回帰で重みが０になるのはなぜ？という点を理解するには、L1ノルムとL2ノルムを理解する必要があります。詳しく知りたい方は、以下の記事を①、②の順に読んで頂くのがオススメです。

①【機械学習】LPノルムってなんだっけ？
②罰則付き・正則化回帰モデルについて（About penalized/regularized regression model）

モデルに含まれる説明変数の数が限定されるとモデルを解釈がしやすく（スパースな解が求められる）なるため、実際どの特徴量（説明変数）が目的変数へ作用する度合いが強いのか、重要であるかが明らかになります。ただ、複数の相関が強い説明変数が存在する場合にはそのグループの中で一つの変数のみを選択してしまうという欠点があるは注意したい点ですね。

また、説明変数（特徴量）の数（p）がモデル構築に使えるデータの数（n）より多い場合(p>n)には、n個の説明変数の効果しか探索することができません（nを選択する必要があります）。 そのため、p＞＞n の場合には十分にデータの傾向やパターンを表現できていないモデルになる可能性があります。

Elastic Net

Elastic Netはリッジ回帰とLasso回帰の折衷案で、「Lasso回帰のモデルに取り込める説明変数の数に制限がある」という問題点をカバーできる方法として作られました。Elastic Netでは、L1正則化項（L1ペナルティ）とL2正則化項（L2ペナルティ）を使用しデータがm個あるとした場合に下記の式で表現されます。

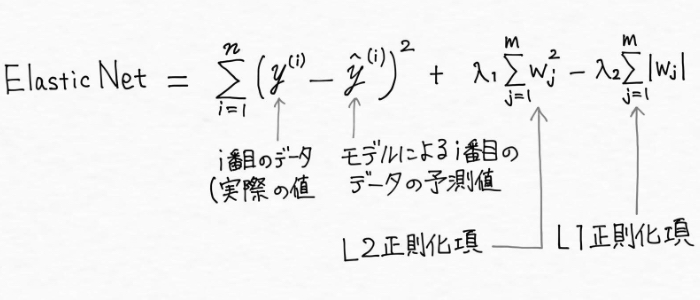
この場合L1正則化項は疎なモデル（スパースモデル：０以外の重みを持つ特徴量がほとんど無いモデル）を生成するために使用され、L２正則化項は選択される変数の個数といったLassoの制約を部分的に克服するために使用されます。

まとめ

つまり、「リッジ回帰」「Lasso回帰」「Elastic Net」とは、

＜参考＞

・Andreas C. Muller and Sarah Guido　(2016).　Introduction to Machine Learning with Python: A Guide for Data Scientists.　O’Reilly Media, Inc.　（アンドレアス・C・ミューラー、サラ・グイド　中田 秀基（訳）(2017).　Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎　株式会社オライリー・ジャパン）
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗（訳）) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』

・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.

・Aurélien Géron (著), 下田 倫大 (監修), 長尾 高弘  (翻訳) (2018). 『scikit-learnとTensorFlowによる実践機械学習』

・統計学と疫学と時々、助教生活

・統計学と疫学と時々、助教生活疫学を専門とする助教の研究に関する備忘録的ページ。

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。