AI(機械学習)の勉強を進めていると「教師なし学習」「クラスタリング」といった単語はよく見聞きするので非常に重要な手法であることはわかります。けれども、これらをどういう目的でどう活用していけば良いのかをうやむやにしている人は意外と多いかもしれません。
※機械学習:AI(人工知能)を実現する技術の一つ。データからそのデータに潜むパターンや傾向を見つけ、見つけたパターンや傾向を元に未知のデータに対しても判定や予測を行っていく技術
というのは極端に言ってしまえば、「教師なし学習」や「クラスタリング」を使わずとも機械学習を回せてしまう場合が大いにありますし、機械学習プログラミングの入門や初期段階で登場するのは「教師あり学習」と呼ばれる別タイプの手法だからです。
※教師あり学習:情報とその正しい判断(答え)をセットにしてコンピュータにデータのパターンを掴ませていく機械学習です
実際、僕自身がAI(機械学習)の勉強を進めながらも「教師なし学習」と「クラスタリング」の理解を曖昧なままに(後回しに)してきました。しかし、将来的にAIエンジニアとして活躍していきたい僕にとって、これらに対する深い理解が絶対に必要であることは間違いありません。
そこで今回は、「教師なし学習」と「クラスタリング」がどのようなものでどんな風に使えるのか!?ということを基本から順番に調べて僕が整理していくことにしました。
そもそも教師なし学習って何?
 まず教師なし学習とは、機械学習のうちの一つの手法で一言でいうと・・・
まず教師なし学習とは、機械学習のうちの一つの手法で一言でいうと・・・
「正解のないデータから共通する特徴をもつグループを見つけたり、データを特徴付ける情報を抽出したりする学習手法」
という説明がよく見られますが、こういう文章の説明文だけだと「うーん・・・よくわからん」というのが正直なところ。。。そこで教師なし学習がどういうものかは具体的に確認しながら整理していきます。
まず、教師なし学習の代表的なものには「クラスタリング」と「次元削減」があるようで、今回は「クラスタリング」を知りたいので(僕が)こちらにだけ焦点を当てていきます。

(一度に両方触れると僕の理解が追いつかずパンクするのは必須 汗。次元削減についてはまた後日整理したいです)
※後日「次元削減」についても整理しました。詳しくはこちら↓
クラスタリングって何?
 まずクラスタリングって何なの?っていう話なんですが、クラスタリングとはデータ間の距離に基づいて類似するデータをグループに分ける教師なし学習です。クラスター分析と呼ばれることもあり、クラスタとはデータの集まり、グループを意味しています。
まずクラスタリングって何なの?っていう話なんですが、クラスタリングとはデータ間の距離に基づいて類似するデータをグループに分ける教師なし学習です。クラスター分析と呼ばれることもあり、クラスタとはデータの集まり、グループを意味しています。
さて、このクラスタリングのイメージですが、例えば「結婚相手に必要なもの」を尋ねるアンケートがあったとしましょう。クラスタリングを使えば、アンケート結果から結婚相手に必要なもの(見た目重視、収入重視、価値観重視など)が近い人たちをまとめるといったことが可能です。
これを図示すると次のようなイメージです。
◯:見た目重視の人、△:収入重視の人、×:価値観重視の人
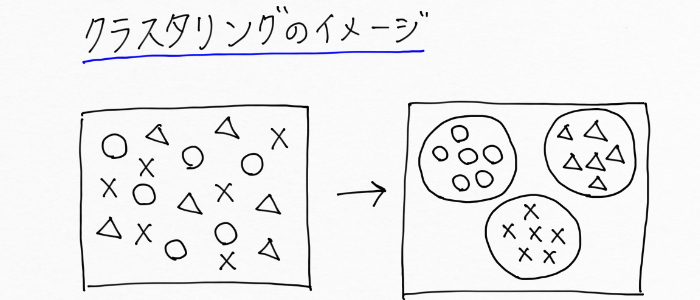
上の左図を見て人間だと目視で「◯」と「△」と「×」の3種類があるなと一瞬で判断できるのですが、コンピュータはそうはいきません。ただクラスタリングという手法を用いれば、「人間がこんな風に分けるんだよ」という正解(教師データ)をコンピュータに提示せずとも、上の右図のようにコンピュータが自動でグルーピングできちゃう!というわけですね!

正解(教師データ)を伴わない機械学習であるため、こうしたクラスタリングの処理は教師なし学習と呼ばれているんですね!
調べたところ、現実においてクラスタリングは次のようなことに利用されているようです。
- 購買データから購買行動が似ているユーザーをグルーピングする
- アンケートデータからユーザーの思考を抽出する
- 文書データの集合からトピックを抽出する
さて、教師なし学習であるクラスタリングのイメージについては見てきましたが、
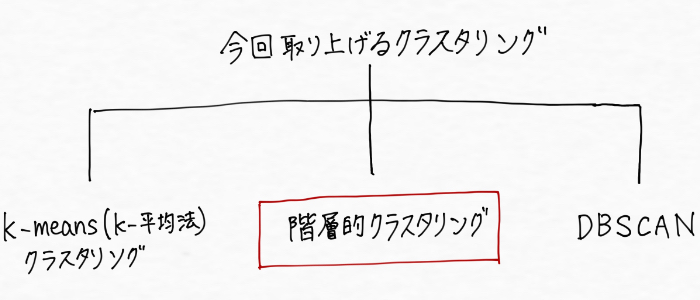
コンピュータは正解となる教師データ無しにどうやってグルーピングしてんの?つまり、どうやってクラスタリングをしてんの?という疑問が残ります。この点について調べてみると、クラスタリングには代表的な3つの種類(グルーピングのやり方がそれぞれ違う)が出てきました。その名も・・・
- k-means(k-平均法)クラスタリング
- 階層的クラスタリング
- DBSCAN
という3つです。今回はこの3つを整理していきます!
k-means(k-平均法)クラスタリング
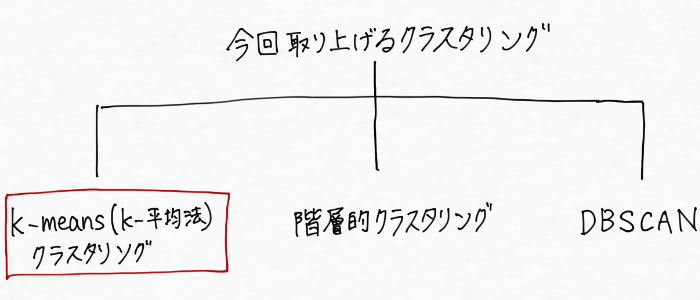
まず一つ目のクラスタリングは、k-means(k-平均法)クラスタリングです!こちらは最も単純で最も広く使われているクラスタリングアルゴリズムで、シンプルな手法でデータの傾向を見るのによく使われます。
k-meansを使うと、例えば次のデータがあった場合に、
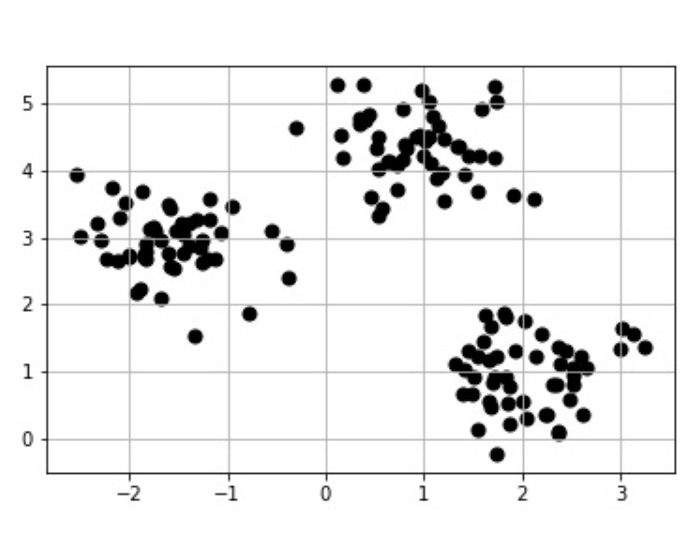
じゃーん!!!
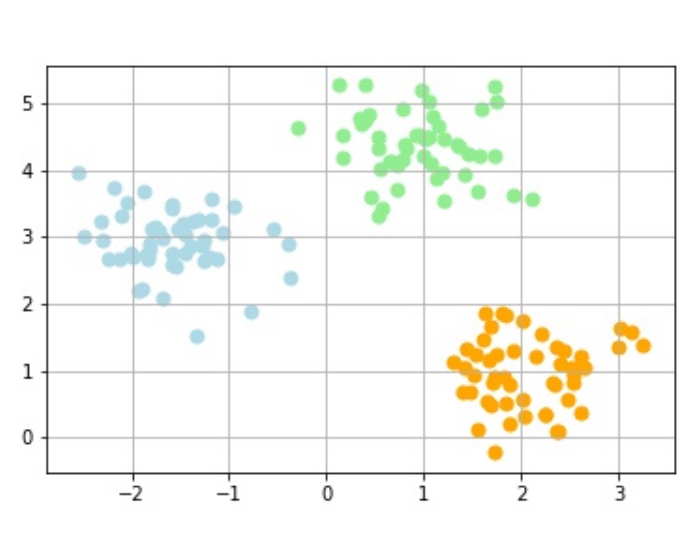
こんな風にデータが分類されるわけです!
k-meansクラスタリングの処理の流れ
k-meansクラスタリングの処理の流れを調べて整理しました。k-meansクラスタリングは次のように動作しています!
- クラスタ(グループ)の中心の初期値として、データポイントからk個の類似するデータの中心(セントロイドと言います)をランダムに選ぶ。(クラスタの中心点をk個ランダムにとる)
- 各データポイントを最も近いセントロイドに割り当てる
- セントロイドに割り当てられたデータポイントの中心にセントロイドを移動する
- データポイントへのクラスタの割り当てが変化しなくなるか、ユーザー定義の許容値(セントロイドの移動がある数値未満になったら処理を止めましょうなど)、または処理の繰り返しの最大回数に達するまで②〜④を繰り返す
上記の処理の流れはこちらの動画で確認できます

参考書によってクラスタリングを適用するデータポイントに対する呼び名が次のように異なっていました。「データポイント」、「データ点」、「観測値」、「サンプル」。これらは全て同じものを指していると思われます。
k-meansクラスタリングの利点と欠点
k-meansクラスタリングには次のような利点と欠点があります。
<利点>
- 階層構造を持たないため、データ量が多い場合に有効
<欠点>
- データ毎に最適なクラスタ数を指定してあげる必要がある
- まず初めにどこをクラスタの中心にするかというクラスタの中心の初期値をランダムに選ぶため、 アルゴリズムの出力結果が初期値に依存してしまう
- クラスタに関して全ての方向が同じように重要であると仮定してグルーピングを行っていくため、球状(または円状)のクラスタでないと識別できず、例えばtwo_moonsのような複雑な形にはうまく機能しない。具体的には、次のtwo_moosというデータセットに
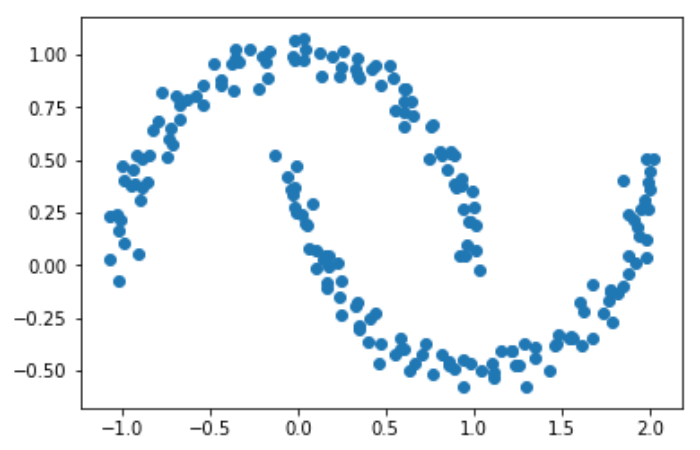
k-meansを適用すると次のように分類されてしまって明らかにうまく分類できてません 汗
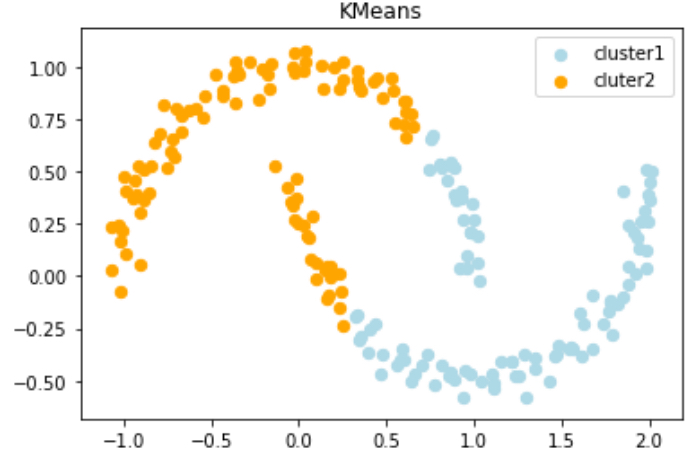
k-meansを試してみる
k-meansはを利用するコードを書いてみました。
最適なクラスタの個数kってどうやって決めればいいの?
ここまでk-meansクラスタリングについて整理してきたわけですが、ここでめっちゃ気になる点が一つあります。。それは、、、
そもそも最適なクラスタの個数kってどうやって決めたらいいの!?
ということです!だって考えてもみてください。データが2次元、3次元だったら可視化してデータの形を確認できるけど、機械学習でよく取り扱う高次元のデータだったらそのまま可視化なんてできません。だからクラスタがいくつありそうかなんてそんなもん検討もつきませんよ・・・(´;ω;`)
しかし諦めてはいけません。こんな非常に悩ましい点の解決に貢献してくれるヒーロー・・・・いました!!それは、、、
「エルボー法」と「シルエット分析」
という2大ヒーローです!!で、具体的に「エルボー法」と「シルエット分析」って何なの?ってなるのは山々なんですが、これらの理解を深めるには、k-meansの性能を数値化するSSEという指標について理解しておく必要があるので、一旦SSEについてここで整理していきます。
k-meansの性能を数値化する指標「SSE」って何?
 SSEは別名、クラスタ内誤差平方和と呼ばれるもので、様々なk-meansクラスタリングの性能を評価できる一つの指標です。SSEは、各データポイントと属しているクラスタのセントロイドとの距離(ユークリッド距離)の総和を意味しています。
SSEは別名、クラスタ内誤差平方和と呼ばれるもので、様々なk-meansクラスタリングの性能を評価できる一つの指標です。SSEは、各データポイントと属しているクラスタのセントロイドとの距離(ユークリッド距離)の総和を意味しています。
※ユークリッド距離:ある点と点を定規で測るような、僕たちが普段想像するような距離。
つまり、SSEの値が小さければ小さいほど各データポイントがセントロイドに近いことになり、「中心から近いところに位置しているからきっとこれらは同じグループに違いない」とk-meansクラスタリングが処理するというわけですね!なるほど!
最適なクラスタの個数を推定するエルボー法
 さて、ようやくたどり着きました。
さて、ようやくたどり着きました。
k-meansに指定する最適なクラスタ数kをどのように決定すれば良いのか。そんな僕たちのお悩みを解決してくれるヒーローの一人目は、エルボー法と呼ばれる手法で、これを使えば最適なクラスタ数kを推定することができます!!
エルボー法は、クラスタ数を増やしていった時にSSE(クラスタ内誤差平方和)がどのように変化するかを視覚化し、その結果からk-meansの最適なクラスタ数を決定する手法です。(なんて便利なんだありがとう!!)
クラスタ数とSSEの関係を次の図のように視覚化すると、SSEの値が肘のように急に曲がる点があり、この時のクラスター数が最適なものと判断できるというわけですね。
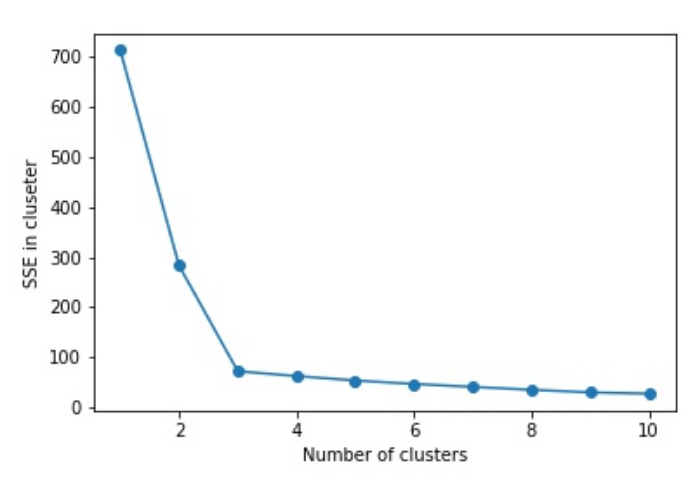
上の図からわかる通り、クラスタ数を増やせば増やすほどSSEは小さくなっています。これはクラスタ数を増やすほど、各データポイントがそれらの割り当て先であるクラスタのセントロイドに近くなるということで納得できますよね。(SSEは各データポイントと属しているクラスタのセントロイドとの距離の総和でした)
ただ、現実的には上の図のような綺麗な図はほとんど得られないとのこと・・・(マジか・・・) 汗
そしてエルボー法は次のように利用できます。
クラスタ数別にクラスタリングの性能を評価する指標シルエット分析
エルボー法に続いて、クラスタリングの性能を評価するためのもう一人のヒーロー(指標)は、シルエット分析です!
シルエット分析はk-means以外のクラスタリングアルゴリズムにも適用でき、クラスタ内のデータポイントがどの程度密にグループ化されているかの目安となるグラフをプロットしたものです(文章だけだとわかりづらいのでもちろん後に図も載せてます)。
ここでイメージしてみると、適切にグルーピングされたクラスタは、同じクラスタに属するデータポイントとの間の距離は小さく(密集している)、別のクラスタに属するデータポイントとの距離は大きいはずですよね。
シルエット係数はこれらを1つの値で表現し、次の数式で表現されます。
※任意のデータポイントを、データポイントiとして、
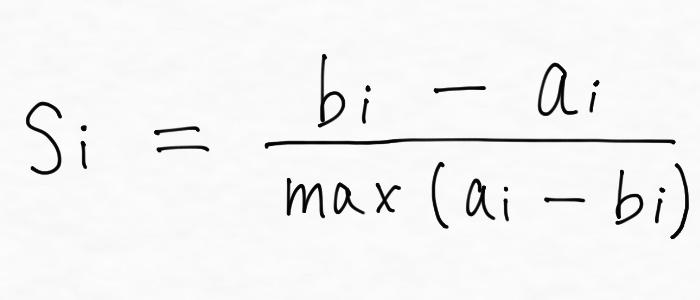
si:データポイントiのシルエット係数
ai:データポイントiと同じクラスタに分類された全てのデータポイントとデータポイントiとの距離の平均
bi:データポイントiと他のクラスタのうち最も近いクラスタのデータポイントとの距離の平均
max(ai, bi):aiとbiのどっちか大きい方
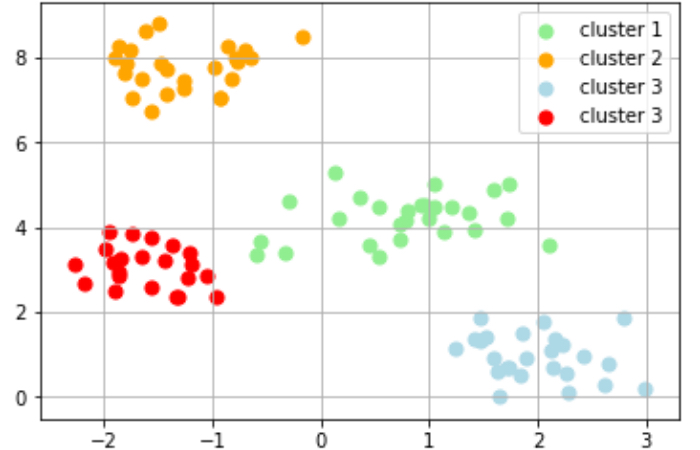
シルエット係数は-1と1の間の数値をとり、1に近いほど密でよく分離されたクラスタと判断できます。このシルエット係数をどのように活用していくかというと、例えばk-meansクラスタリングを適用して次のように3つにグルーピングされたデータがあった時、
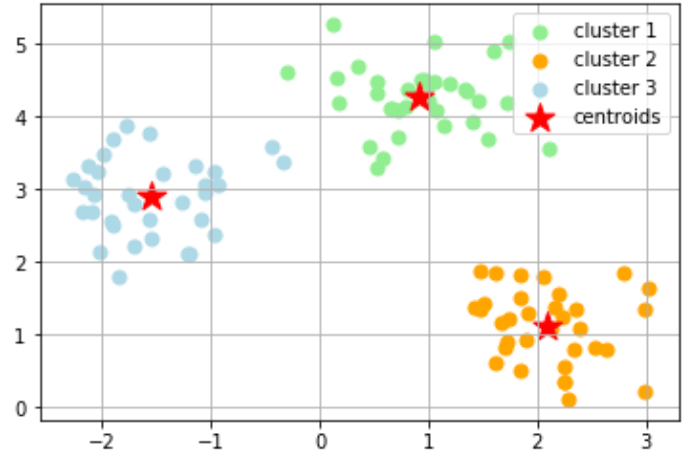
この場合の各クラスタに関するシルエット係数を横軸に、縦軸をクラスタのラベルとしたシルエット図は次のようになります。
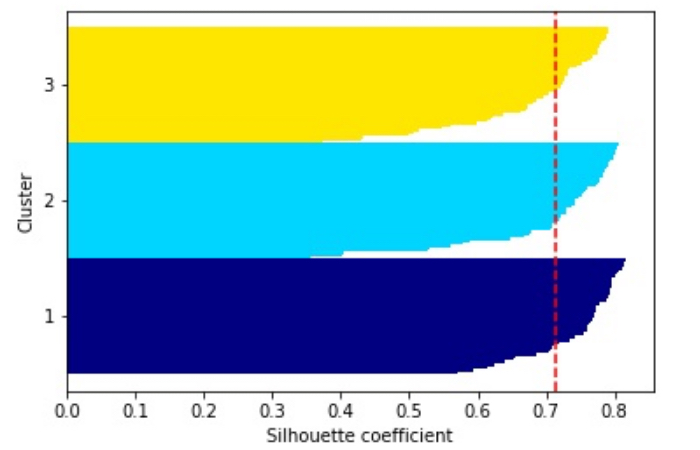
このシルエット図の意味を理解するのに大変苦戦したのですが、この図は各クラスタがどれだけ密で且つ他のクラスタからよく分離されているかを示しているんですね。
ナイフの先のような形をしたものが3つ見えるのですが、これはクラスタ毎に各データポイントのシルエット係数を一つ一つ棒グラフで表現してソートしたものです。シルエット係数は1に近いほど密でよく分離されたクラスタと判断されます。
一方で、例えば次のように不適切なクラスタ数を設定してk-meansクラスタリングを行なった場合には、
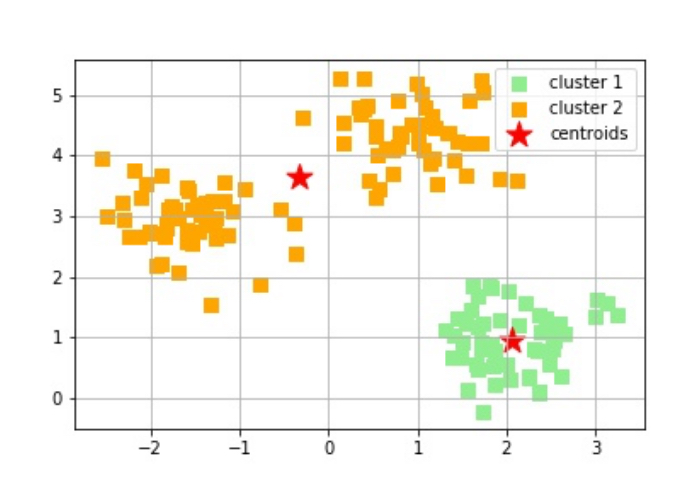
シルエット図は次のようになります。
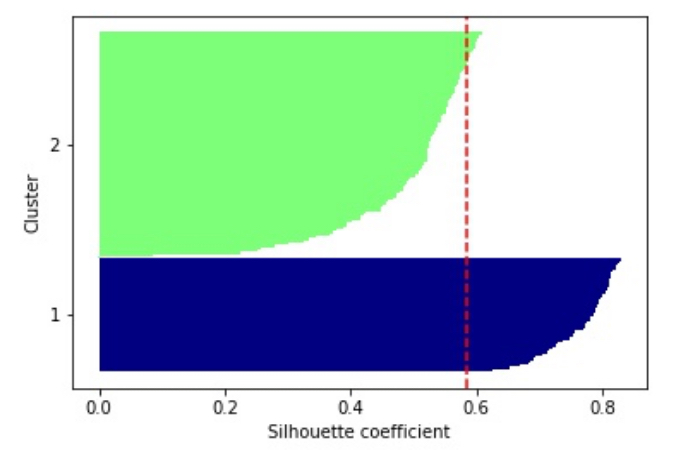
上図をみると、2のラベル付けがされたクラスタのシルエット係数が非常に低いので、上手くクラスタリングできていない=クラスタ数の設定に問題があることが判断できますよね。以上がシルエット分析です。
最後に、シルエット分析は次のように利用できます。
階層的クラスタリング
 k-meansクラスタリングの次に見ていくのは、階層的クラスタリングです。
k-meansクラスタリングの次に見ていくのは、階層的クラスタリングです。
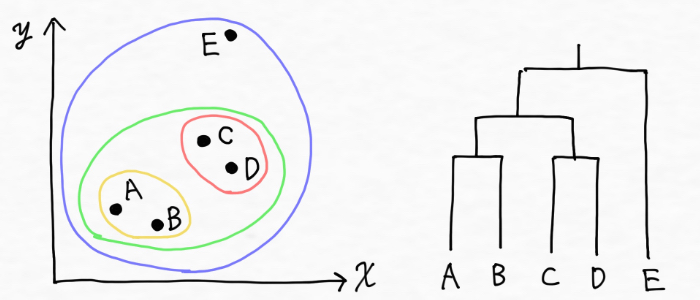
階層的クラスタリングとは、データの中から最も似ている組み合わせを探し出し順番にクラスターにしていく方法です。途中過程で階層構造になることが特徴としてあり、最終的に下の右図のような樹形図(デンドログラム)が構成されるため、多次元のデータセットであってもどのようにデータポイントがクラスタに分けられたのかを理解できます。
<階層的クラスタリングのイメージ>
2種類の階層的クラスタリング
階層的クラスタリングには、凝集型と分割型の二つのアプローチがあります。
- 凝集型階層的クラスタリング
個々のデータポイントを一つのクラスタとして扱い、クラスタが一つだけ残った状態になるまでマージ(併合)していく。 - 分割型階層的クラスタリング
全てのデータポイントを含む1つのクラスタを定義し、そのクラスタをどんどん分割していって全てのクラスタにデータポイントが一つだけ含まれた状態になるまで分割をしていく。
今回は凝集型階層的クラスタリングに焦点を当てていきます。
凝集型階層的クラスタリングの処理の流れ
凝集型階層的クラスタリングは、次の手順でデータをグルーピングしていきます。
- 個々のデータポイントをそれ自身が1つのクラスタであるとみなす
- 何らかの条件(後述)で2つのクラスタを選択し、それらを併合する
- これを指定した数のクラスタだけが残るまで繰り返す
<凝集型階層的クラスタリングが進む様子のイメージ>
凝集型階層的クラスタリングによる処理が進んでいくイメージは次の動画がわかりやすいです。デンドログラム(樹形図)が登場しますが、こちらについては以降で整理していきます。
階層的クラスタリングの利点と欠点
階層的クラスタリングには次のような利点と欠点があります。
<利点>
- 樹形図(デンドログラム)をプロットでき、データの階層的な分割の候補を全て提示するため結果を解釈するのに役立つ
- 最適なクラスタ数を選択する手助けをしてくれる
<欠点>
- k-meansクラスタリングと同様に、two_moonsのような複雑な形状はうまく扱うことができない
凝集型階層的クラスタリングを試してみる
凝集型階層的クラスタリングは次ように利用できます。
樹形図(デンドログラム)を用いてクラスタリングの結果を解釈できる
樹形図(デンドログラム)という方法を用いれば、例えば次のように凝集型階層的クラスタリングの結果を解釈してデータにおける共通する特徴をもつグループや関係性を掴むことができます。(これは便利!!)
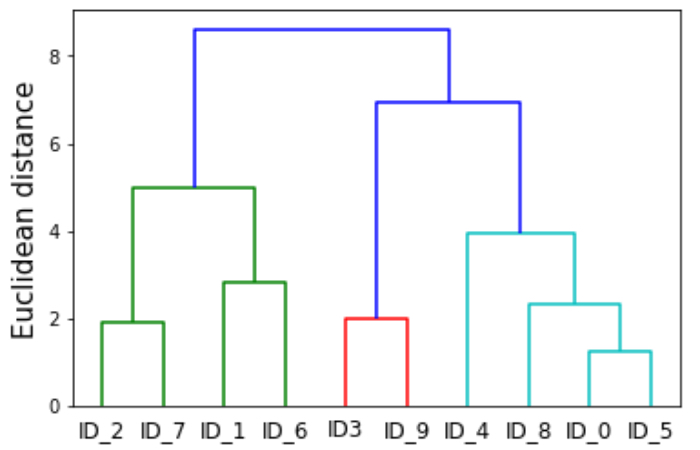
樹形図(デンドログラム)のy軸は、凝集型クラスタリングアルゴリズムが2つのクラスタを併合したかとどれだけ離れていたかを示しています。上図の一番上で2つのクラスタを一つにまとめていますが、この時には比較的遠く離れたクラスタを併合していることがわかります。
上記の樹形図(デンドログラム)は次のように利用できます。
DBSCAN
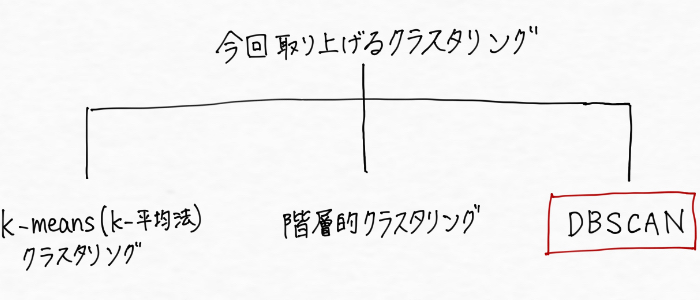 k-meansクラスタリング、階層的クラスタリングときて、最後はDBSCANです!DBSCANは、Density-based Spatial Clustering of Applications with Noiseの略だそうです・・・な、なげえ。。日本語訳は、「密度に基づくノイズあり空間クラスタリング」とのこと。
k-meansクラスタリング、階層的クラスタリングときて、最後はDBSCANです!DBSCANは、Density-based Spatial Clustering of Applications with Noiseの略だそうです・・・な、なげえ。。日本語訳は、「密度に基づくノイズあり空間クラスタリング」とのこと。
このDBSCANはクラスタ内では多くのデータポイントが密に集合しているはずだ!という考えに基づいていて、k-meansクラスタリングでも凝集型階層的クラスタリングでもうまく扱えなかったtwo_moonsのような複雑な形状をうまく扱えます!٩( ‘ω’ )و
ちなみにtwo_moonsとはこんなデータセットでした↓

そんな嬉しいDBSCANを整理していきましょう!
DBSCANの処理の流れ
DBSCANは次のようにクラスタリングを実行していきます。
- データポイントxiをランダムに選択する
- xiの近傍点を探す(xiを中心に半径ε以内)。見つかった近傍点の数が指定した数(MinPts)よりも大きければ、これらがクラスタを構成しているとみなす (※εはイプシロンと読みます)
- xiの近傍点に対して同じ動作を繰り返してクラスタを拡大する。これらがクラスタのコアポイントとなる。
- ③で近傍となるデータポイントがそれ以上なくなったら、①に戻って新しいデータポイントをランダムに選択する
- 上記の過程が終了すると、いくつかのクラスタとそのコアポイントが得られる。最後にクラスタに近いけれどコアポイントではないデータポイントをクラスタに含め、どのクラスタからも遠いデータポイントはノイズポイント(外れ値)とする。
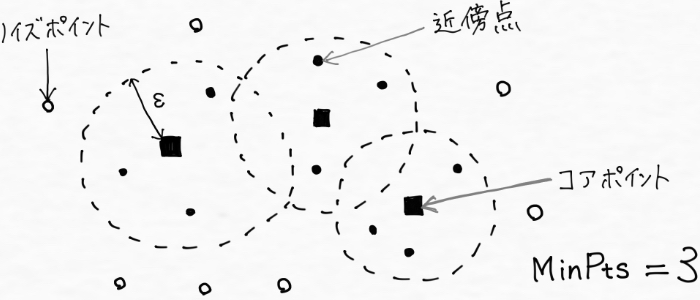
ここまでの手順の内容を図示すると次のイメージです。
※ノイズ点:ノイズポイント
※コア点:コアポイント
DBSCANの処理の様子はこちらの動画で確認できます
階層的クラスタリングの利点と欠点
調べてみると、DBSCANの主な利点と欠点は下記の通りです。
<利点>
- ユーザがクラスタ数を先験的に与える必要がない
- どのクラスタにも属さない点を判別できて外れ値を除去できる
- k-meansのようにクラスタが球状であることを前提としない
<欠点>
- データポイントがどれだけセントロイドに近いか、つまり密度を閾値としてクラスタリングを行うため、クラスタ間で密度が異なるようなデータに対して上手くクラスタリングできないことがある
DBSCANを使ってみる
DBSCANを利用するためのコードを書いて、two_moonsのデータセットを作成してk-meansクラスタリング、階層的クラスタリング、DBSCANの3つを比較してみました。
two_moonsのデータセットに対する各クラスタリングの結果は、、
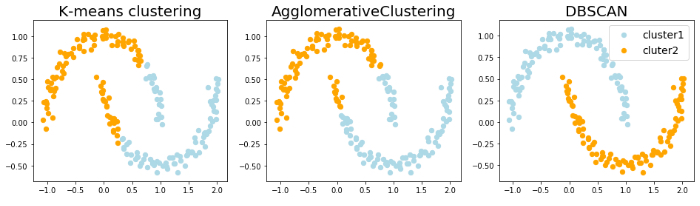
百聞は一見に如かず。DBSCANだけが半月状のクラスタをうまく検出できています。DBSCANが、任意の形状を持つデータのクラスタリングだという特徴がよくわかりますよね!!
まとめ
さて、今回はクラスタリングの基本ということで、「k-meansクラスタリング」「階層的クラスタリング」「DBSCAN」という3つのクラスタリングについて整理してきました。ざっと内容を振り返ってみると、
まずk-meansは、指定した個数のクラスタのセントロイド(クラスタの重心)に基づいて、データポイントが球状にクラスタリングされました。クラスタリングの性能を数値化するためには、エルボー法やシルエット分析といった便利な性能指標がありましたよね!
次に階層的クラスタリングは、クラスタの個数を事前に指定する必要がなく、クラスタリング結果が樹形図(デンドログラム)として表示できるため、結果を解釈するのに役立ちました。
そしてDBSCANは、局所的な密度に基づいて点をグループ化するアルゴリズムであり、外れ値を処理できるほか、two_moonsのような球状以外の形状を上手く識別できました!
たくさんの内容を整理してきたのですが、これで教師なし学習って何?クラスタリングって何なの?という疑問は解決できました(僕が)。ただ、「わかった!」と思っても「・・・やっぱり使えない(´;ω;`)」となることはよくあるもので、実際僕はそれで会社をクビになったこともありました。
その時の話はこちら
誰もが実感しているように、インプットはアウトプットがあってこそ活かされますし、知識が自分のものとなります。次は今回学んだ内容を実際に自分で使ってみる!そんなステップへと進んでいきたいですね(^^)
今回は教師なし学習の代表的なものであるクラスタリングについて深掘りしてきましたが、今回取扱えなかった「次元削減」についても今後整理していきます。よかったらまた覗きにきてください(^^)

AI(人工知能)って「なにそれ美味しいの?」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください(実話)。
<参考>







コメントをどうぞ