ゼロからわかるAI（機械学習）モデルの評価に役立つ混同行列とは

実用的なAI（機械学習）モデルをつくるには訓練データを用いて学習させていく必要がありますが、目的達成に繋がる適切なモデルかどうかを判断するにはただ精度だけを見るのでは危険です。

※モデル：ある事象を簡略化して本質を表したもの（パターンやルールを数式で表現したもの）です

※訓練データ：実用的なAI（機械学習）モデルを作るために、モデルを訓練させるために用いるデータです

※学習：データの傾向やパターンを適切に表現するモデルを構築していくことです

AI（人工知能）はあくまで問題解決のためのツールなので、解きたい問題やテーマに応じて適切な性能評価が求められます。そこで今回は、性能評価の中でも代表的な存在である「混同行列」という行列についてお伝えしていきます。

一言で言うと「混同行列」とは・・・

4つの領域から構成される混同行列

混同行列は、「予測結果がどうだったか」と「実際どうだったか」の関係を示す行列で、次のような形をしています。

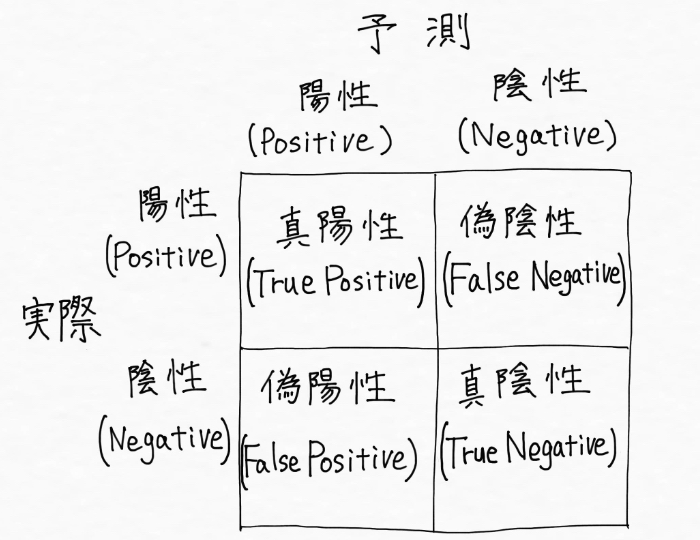
陽性＝Postive, 陰性＝Negative、予測が当たった→真 = True、予測が外れた→偽 = Falseという意味です。

混同行列の内容を具体的に整理すると、

真陽性（TP）：実際陽性であるものを陽性だと予測した

偽陰性（FN）：実際陽性であるものを陰性だと予測した

偽陽性（FP）：実際陰性であるものを陽性だと予測した

真陰性（TN）：実際陰性であるものを陰性だと予測した

となり、上の図を略称表記にして見やすく整えると次のようになります。

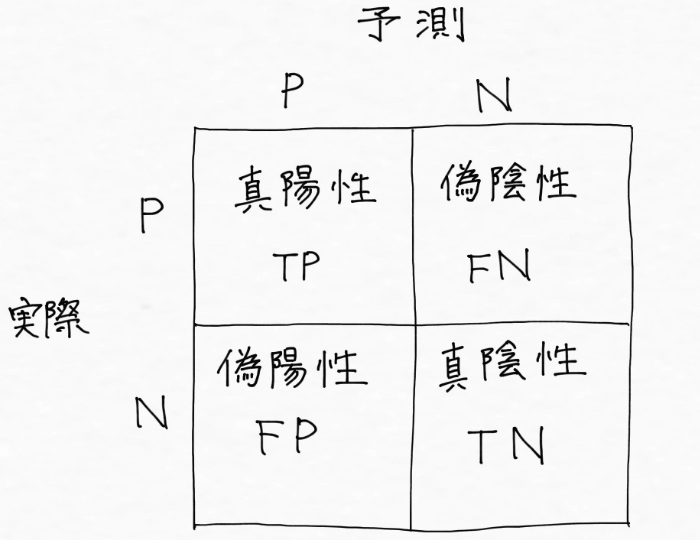
この混同行列から、

• モデルによって予測したものが実際どれだけ的中したのかの割合を表す「正解率（精度）」
• 陽性だと予測したもののうち実際に陽性だった割合を示す「適合率」
• 実際に陽性だったものを陽性だと予測できた割合を示す「再現率」
• 「適合率」と「再現率」のバランスを示す指標である「F値（F-measure、F1スコア、F尺度）」

が算出でき、これらを元に機械学習モデルの性能を評価することできます。

つっちー

もっと詳しく知りたい方はこちらの記事がオススメです！↓

AIは学習後が超大事！ゼロからわかる機械学習モデルの性能評価Part1

「AI（機械学習）の予測精度が95%！」なんて聞くと「すごい！」と思ってしまいがちですよね。けれど精度に注目するだけでは不十分で、適切な性能評価の手法を理解しておかなければ実用的な機械学習モデルを構築することはできません。そこで今回はAI（機械学習）モデルの性能評価に関する知識を整理していきます！！

aizine.ai

まとめ

つまり、「混同行列」とは

＜参考＞

・Andreas C. Muller and Sarah Guido　(2016).　Introduction to Machine Learning with Python: A Guide for Data Scientists.　O’Reilly Media, Inc.　（アンドレアス・C・ミューラー、サラ・グイド　中田 秀基（訳）(2017).　Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎　株式会社オライリー・ジャパン）
・Sebastian Raschka(2015). Python Machine Learning. Packt Publishing. (株式会社クイープ、福島真太朗（訳）) (2016). 『Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)』

・松尾 豊(2015, 西林 孝(2018).『仕事ではじめる機械学習』株式会社オライリー・ジャパン.

・Antonio Gulli (著), Sujit Pal (著), 大串 正矢 (翻訳), 久保 隆宏 (翻訳), 中山 光樹 (翻訳) (2018).『直感 Deep Learning ―Python×Kerasでアイデアを形にするレシピ』

つっちー

AI（人工知能）って「なにそれ美味しいの？」ってレベルだった僕が、AIエンジニアを目指してステップを踏んだり踏まれたりしている記事を書いてます。よかったら読んでみてください（実話）。