機械学習では様々な手法で損失関数を最小化していきますが、最小化の手法について詳しく解説しているメディアはあまり多くはないですよね。本記事では最小化問題を解く手法のひとつである、勾配降下法(こうばいこうかほう)について説明していきましょう。
※「勾配降下法」という名前からして理解するのも難しそうなイメージを抱きがちですが、決してそんなことはありません。
勾配降下法とは
最小化したい関数がある場合にその関数の勾配を求め、その勾配を元に関数の最小値を探索する手法です。
では早速勾配降下法を用いて関数y=x^2の最小値を求めてみましょう。y=x^2は以下の図で表される形をしておりyの最小値は0です。
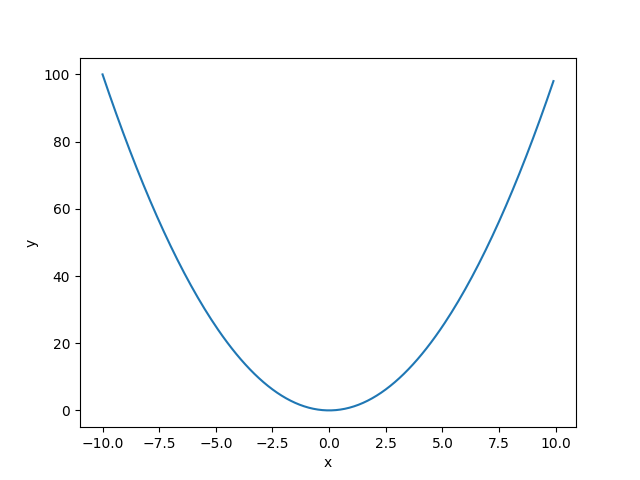

y=x^2
勾配降下方による最小値の探索の様子をGIFファイルにしてみました。このGIFは以下のコードを実行して得られた結果です。
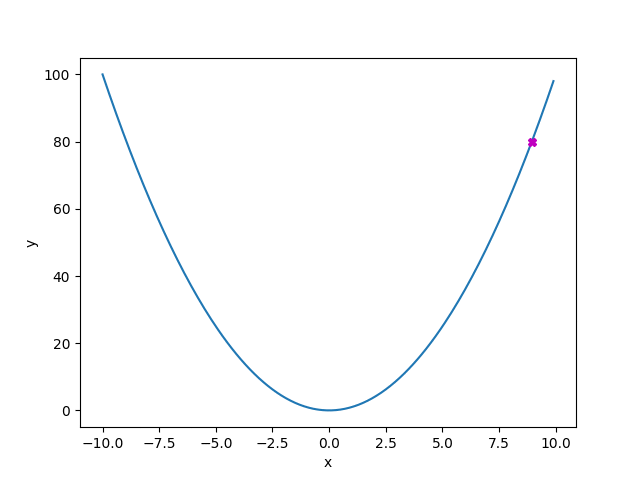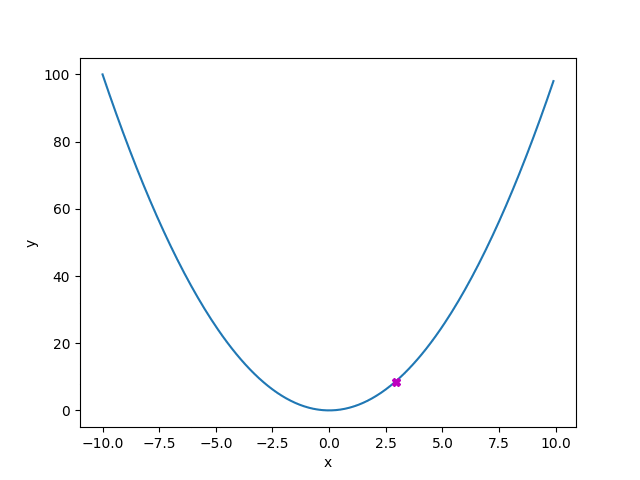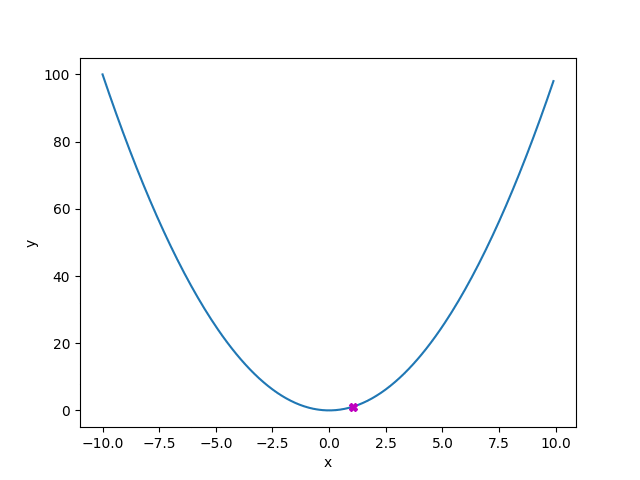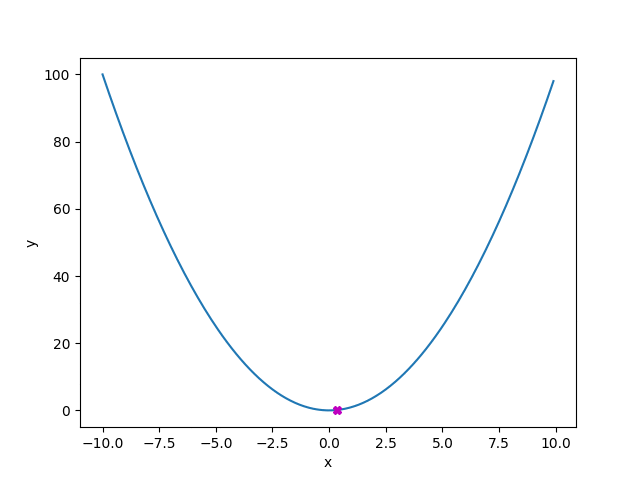

gradient_descent
import matplotlib.animation as animation
import matplotlib.pyplot as plt
import numpy as np
def objective(x):
return x**2
def differential(func, x):
h = 1e-4
diff = (func(x + h) - func(x)) / h
return diff
if __name__ == '__main__':
x = np.arange(-10, 10, 0.1)
y = objective(x)
ans = 100
lr = 0.1
plots = []
fig = plt.figure()
plt.plot(x, y)
for i in range(30):
diff = differential(objective, ans)
ans -= lr * diff
line, = plt.plot(np.sqrt(ans), ans, color='m', marker='X')
plots.append([line])
ani = animation.ArtistAnimation(fig, plots)
ani.save('gradient_descent.gif', writer='imagemagick')
plt.show()
勾配降下法の種類
勾配降下法は学習データをどのように利用してパラメータを更新するかによって、いくつかの名称があります。
- バッチ勾配降下法(最急降下法)
- ミニバッチ勾配降下法
- 確率的勾配降下法
バッチ勾配降下法(最急降下法)
バッチ勾配降下法はパラメータの更新のたびに全ての訓練データで勾配を計算します。バッチ勾配降下法により100件や1000件程度のデータであれば全てのデータを同時に計算しても問題はありません。しかし、訓練データの量が増加するにつれて計算を行うのが難しくなるため、その場合はミニバッチ勾配降下法や確率的勾配降下法を利用します。
ミニバッチ勾配降下法
ミニバッチ勾配降下法は一度に利用する訓練データの量がバッチ勾配降下法と比較して少なくなっている(ミニ)ことから命名されており、訓練データの中からいくつかのデータを取り出し、そのデータで計算した勾配に基づいてパラメータを更新する手法です。バッチ勾配降下法と比較して計算に必要なメモリ量が少ないこと、後ほど紹介する確率的勾配降下方と比較して外れ値の影響を受けにくく学習が比較的安定して進むという利点があります。
確率的勾配降下法
確率的勾配降下法は訓練データの中からひとつのデータを取り出し、そのデータから計算した勾配を用いてパラメータを更新していく手法です。毎回の勾配の更新がひとつのデータから行われるので計算量が少なく済むという利点がある一方で、外れ値などの影響を受けやすくなるため毎回のパラメータの更新が安定しないという問題がある点は無視できません。
勾配降下法比較表
勾配降下法で用いられるバッチ勾配降下法、ミニバッチ勾配降下法、確率的勾配降下法について以下の表に、「利用するデータの量」、「毎回の更新に必要な計算量」、「計算される勾配の安定性」についてまとめました。
利用するデータの大きさに伴って計算量が増加し、勾配が安定していくという構図になります。
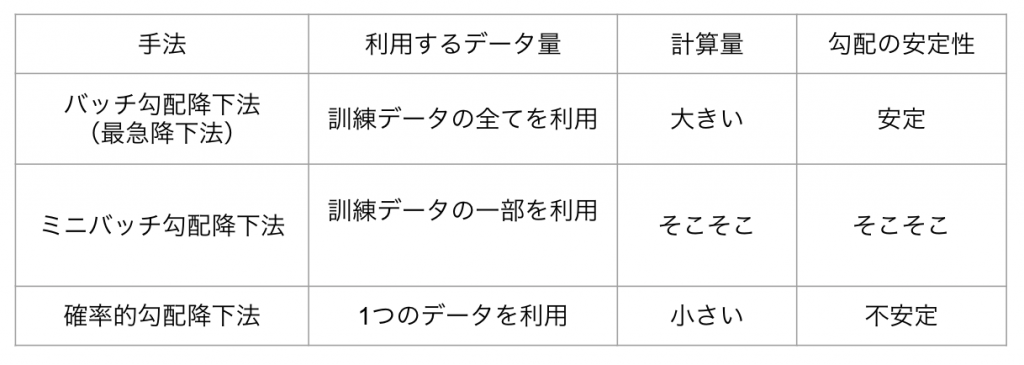

勾配降下法比較表
まとめ
勾配降下法について重要な点をまとめましょう。
- 勾配降下法はある関数の最小値を求めるための手法のひとつ
- 勾配降下法にはバッチ勾配降下法(最急降下法)、ミニバッチ勾配降下法、確率的勾配降下法の3つの種類がある
- 線形回帰などの機械学習の学習で広く利用される




