機械学習でモデルが学習データに過剰にフィットしてしまい、検証データやテストデータに対する性能が落ちてしまう現象を過剰適合やオーバーフィッティング、過学習と呼びますよね。本記事ではこの問題を解決するための手法である正則化について解説していきましょう。
正則化とは
二乗誤差を最小化することで学習を行う回帰モデルを例に考えましょう。この回帰モデルに正則化を行う場合は二乗誤差の式に正則化項と呼ばれる項が追加されます。以下の式が単純な二乗誤差を表す式です。
これにalphaの係数を持つ正則化項を加えることで以下のようになります。
この正則化項付きの損失関数を最小化することで、正則化項がない場合よりも過剰適合がしにくくなるというのが正則化のざっくりとした説明です。
ではこの正則化項があることで何が変わるのでしょうか。数式のイメージを定性的に捉えていいように解釈すると、モデルの重みが大きくなりすぎないような制約が追加されることで、特定の特徴量に大きく依存することがなくなり、汎化性能が向上すると考えることができます。次の章では実際にそのような効果があるのかを、簡単な多項式フィッティングの問題を正則化がある場合とない場合で解きながら考えていきます。
正則化の有無による違い
本章では多項式フィッティングの問題を線形回帰で解き、その時の正則化項の有無でどのような違いが出るのかを検証していきましょう。重みに対するL2ノルムを正則化項として加えた線形回帰モデルのことを、Ridge回帰と呼びます。
求めたい真の関数ノイズを加えて生成したデータセット(図中の青の×印)に対して、単純に二乗誤差を最小化した正則化項がない場合の予測結果(図中のオレンジの曲線)、alpha=1.0の正則化項を加えた二乗誤差を最小化した場合の予測結果(図中の赤の曲線)をプロットしてみました。
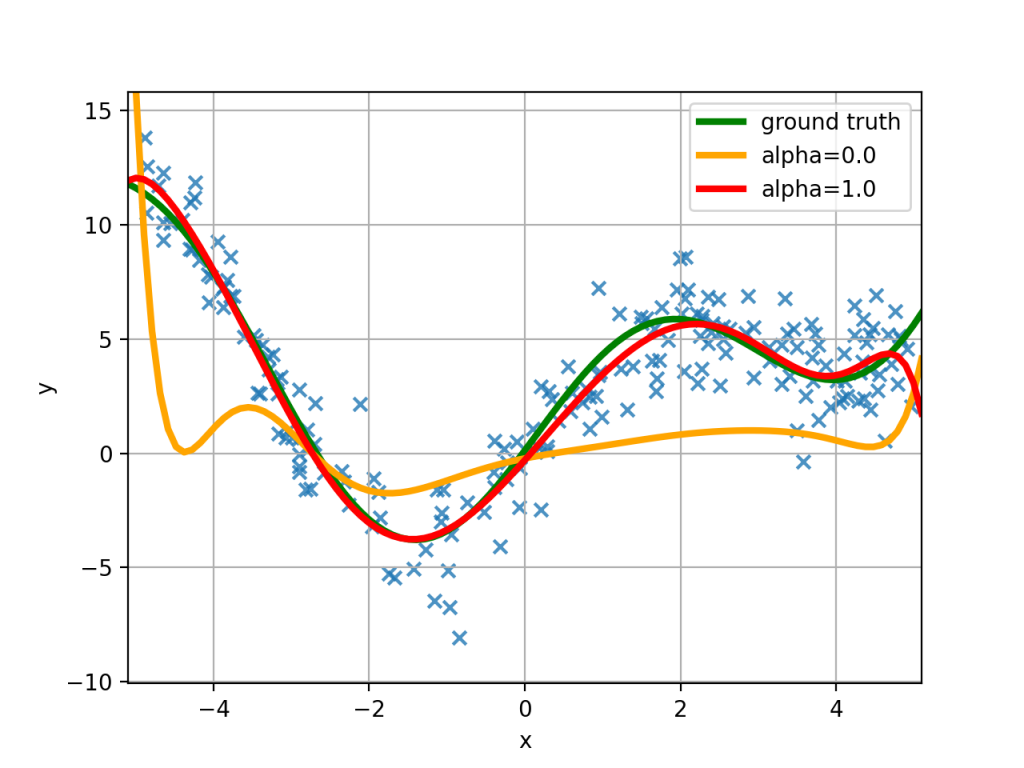

予測したい真の関数が図中の緑の曲線であり、正則化項を導入することでより適切な予測が行えていることがわかりますね。また正則化項を導入していない図中のオレンジの曲線では与えられた学習用のデータセットへの当てはまりは良いのですが、その点に過剰に適合しすぎたあまり、求めたい真の関数とは大きく形が異なってきています。
正則化と深層学習
正則化は先ほどの例のような単純な多項式フィッティングだけでなく、深層学習などの最先端の機械学習モデルでも利用されています。深層学習の文脈では先ほどのような重みに対する正則化のことを重み減衰(weight decay)と呼び、広く利用されています。
また学習中に任意の確率でニューロン間の結合をなくすドロップアウトも、特定の重みに依存せずに予測を実行できるようになるため、正則化手法の一種と考えることができますね。
まとめ
正則化について重要な点をまとめましょう。
- 過剰適合を防ぐ手段で、予測結果を特定の重みに依存させないことで汎化性能を向上させる
- 単純な線形回帰モデルからブースティング、深層学習などの最新手法まで広く利用されている
- 単純に重みのノルムに制限をかける手法だけでなく、深層学習においてはドロップアウトやバッチ正則化など様々な正則化手法が提案されている




